The ORCA Hub: Explainable Offshore Robotics through Intelligent Interfaces

We present the UK Robotics and Artificial Intelligence Hub for Offshore Robotics for Certification of Assets (ORCA Hub), a 3.5 year EPSRC funded, multi-site project. The ORCA Hub vision is to use teams of robots and autonomous intelligent systems (AIS) to work on offshore energy platforms to enable cheaper, safer and more efficient working practices. The ORCA Hub will research, integrate, validate and deploy remote AIS solutions that can operate with existing and future offshore energy assets and sensors, interacting safely in autonomous or semi-autonomous modes in complex and cluttered environments, co-operating with remote operators. The goal is that through the use of such robotic systems offshore, the need for personnel will decrease. To enable this to happen, the remote operator will need a high level of situation awareness and key to this is the transparency of what the autonomous systems are doing and why. This increased transparency will facilitate a trusting relationship, which is particularly key in high-stakes, hazardous situations.

A 'Gibbs-Newton' Technique for Enhanced Inference of Multivariate Polya Parameters and Topic Models

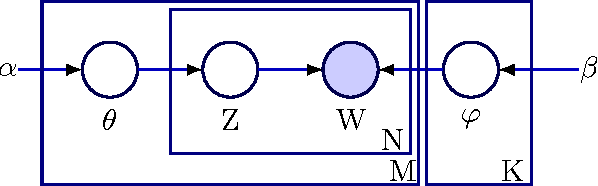
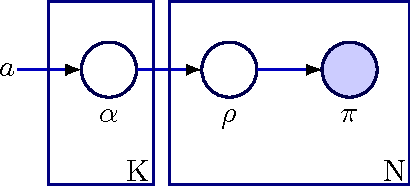
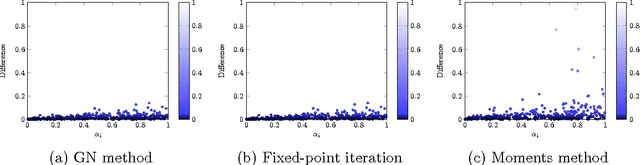
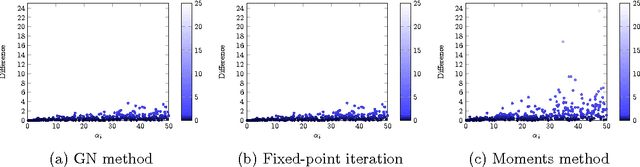
Hyper-parameters play a major role in the learning and inference process of latent Dirichlet allocation (LDA). In order to begin the LDA latent variables learning process, these hyper-parameters values need to be pre-determined. We propose an extension for LDA that we call 'Latent Dirichlet allocation Gibbs Newton' (LDA-GN), which places non-informative priors over these hyper-parameters and uses Gibbs sampling to learn appropriate values for them. At the heart of LDA-GN is our proposed 'Gibbs-Newton' algorithm, which is a new technique for learning the parameters of multivariate Polya distributions. We report Gibbs-Newton performance results compared with two prominent existing approaches to the latter task: Minka's fixed-point iteration method and the Moments method. We then evaluate LDA-GN in two ways: (i) by comparing it with standard LDA in terms of the ability of the resulting topic models to generalize to unseen documents; (ii) by comparing it with standard LDA in its performance on a binary classification task.