David Wolfe Corne
A 'Gibbs-Newton' Technique for Enhanced Inference of Multivariate Polya Parameters and Topic Models
Feb 27, 2016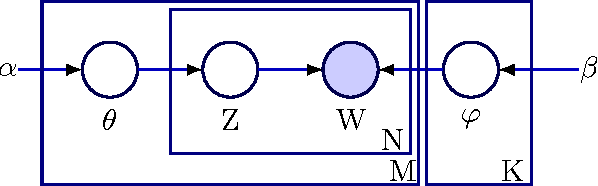
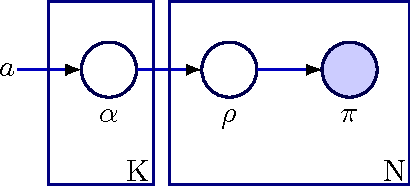
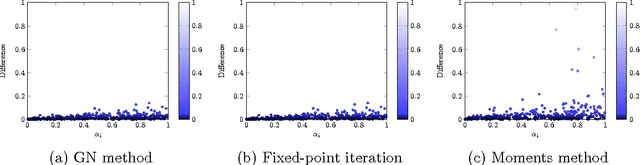
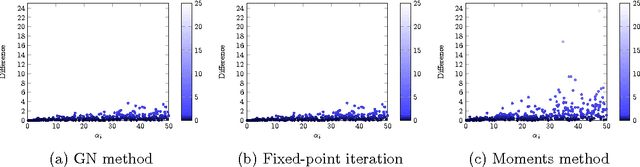
Abstract:Hyper-parameters play a major role in the learning and inference process of latent Dirichlet allocation (LDA). In order to begin the LDA latent variables learning process, these hyper-parameters values need to be pre-determined. We propose an extension for LDA that we call 'Latent Dirichlet allocation Gibbs Newton' (LDA-GN), which places non-informative priors over these hyper-parameters and uses Gibbs sampling to learn appropriate values for them. At the heart of LDA-GN is our proposed 'Gibbs-Newton' algorithm, which is a new technique for learning the parameters of multivariate Polya distributions. We report Gibbs-Newton performance results compared with two prominent existing approaches to the latter task: Minka's fixed-point iteration method and the Moments method. We then evaluate LDA-GN in two ways: (i) by comparing it with standard LDA in terms of the ability of the resulting topic models to generalize to unseen documents; (ii) by comparing it with standard LDA in its performance on a binary classification task.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge