Meike Zehlike
Fair ranking: a critical review, challenges, and future directions
Jan 29, 2022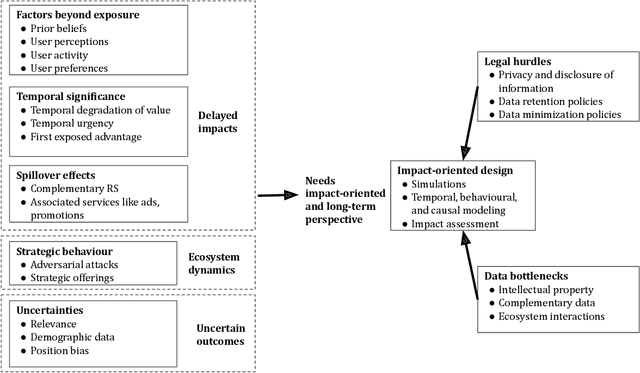



Abstract:Ranking, recommendation, and retrieval systems are widely used in online platforms and other societal systems, including e-commerce, media-streaming, admissions, gig platforms, and hiring. In the recent past, a large "fair ranking" research literature has been developed around making these systems fair to the individuals, providers, or content that are being ranked. Most of this literature defines fairness for a single instance of retrieval, or as a simple additive notion for multiple instances of retrievals over time. This work provides a critical overview of this literature, detailing the often context-specific concerns that such an approach misses: the gap between high ranking placements and true provider utility, spillovers and compounding effects over time, induced strategic incentives, and the effect of statistical uncertainty. We then provide a path forward for a more holistic and impact-oriented fair ranking research agenda, including methodological lessons from other fields and the role of the broader stakeholder community in overcoming data bottlenecks and designing effective regulatory environments.
Fairness in Ranking: A Survey
Mar 25, 2021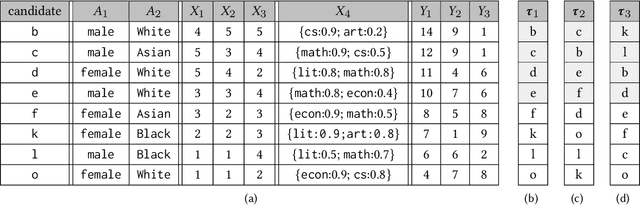

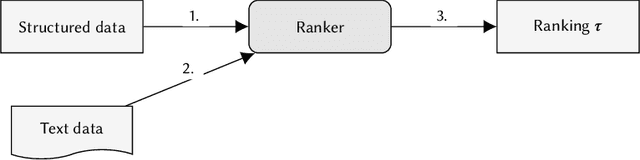
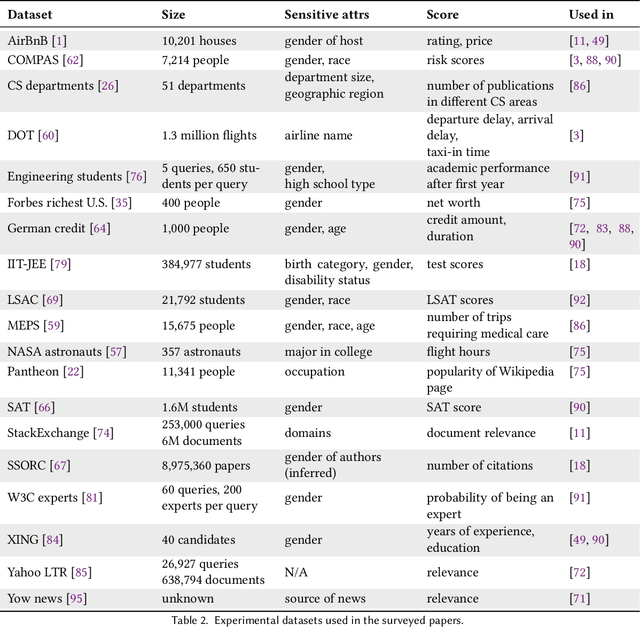
Abstract:In the past few years, there has been much work on incorporating fairness requirements into algorithmic rankers, with contributions coming from the data management, algorithms, information retrieval, and recommender systems communities. In this survey we give a systematic overview of this work, offering a broad perspective that connects formalizations and algorithmic approaches across subfields. An important contribution of our work is in developing a common narrative around the value frameworks that motivate specific fairness-enhancing interventions in ranking. This allows us to unify the presentation of mitigation objectives and of algorithmic techniques to help meet those objectives or identify trade-offs.
A Note on the Significance Adjustment for FA*IR with Two Protected Groups
Dec 23, 2020
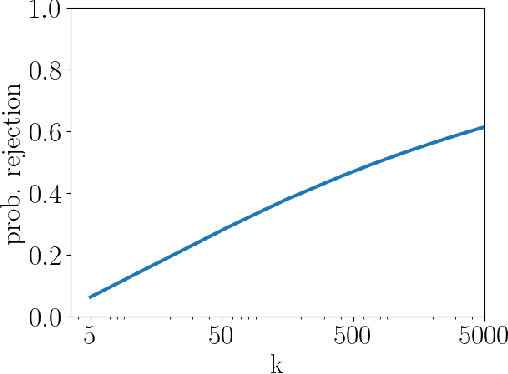
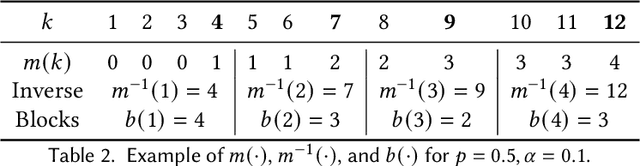

Abstract:In this report we provide an improvement of the significance adjustment from the FA*IR algorithm of Zehlike et al., which did not work for very short rankings in combination with a low minimum proportion $p$ for the protected group. We show how the minimum number of protected candidates per ranking position can be calculated exactly and provide a mapping from the continuous space of significance levels ($\alpha$) to a discrete space of tables, which allows us to find $\alpha_c$ using a binary search heuristic.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge