Comparing Iterative and Least-Squares Based Phase Noise Tracking in Receivers with 1-bit Quantization and Oversampling

High data rates require vast bandwidths, that can be found in the sub-THz band, and high sampling frequencies, which are predicted to lead to a problematically high analog-to-digital converter (ADC) power consumption. It was proposed to use 1-bit ADCs to mitigate this problem. Moreover, oscillator phase noise is predicted to be especially high at sub-THz carrier frequencies. For synchronization the phase must be tracked based on 1-bit quantized observations. We study iterative data-aided phase estimation, i.e., the expectation-maximization and the Fisher-scoring algorithm, compared to least-squares (LS) phase estimation. For phase interpolation at the data symbols, we consider the Kalman filter and the Rauch-Tung-Striebel algorithm. Compared to LS estimation, iterative phase noise tracking leads to a significantly lower estimation error variance at high signal-to-noise ratios. However, its benefit for the spectral efficiency using zero-crossing modulation (ZXM) is limited to marginal gains for high faster-than-Nyquist signaling factors, i.e., higher order ZXM modulation.

Waveforms for sub-THz 6G: Design Guidelines

The projected sub-THz (100 - 300 GHz) part of the upcoming 6G standard will require a careful design of the waveform and choice of slot structure. Not only that the design of the physical layer for 6G will be driven by ambitious system performance requirements, but also hardware limitations, specific to sub-THz frequencies, pose a fundamental design constraint for the waveform. In this contribution, general guidelines for the waveform design are given, together with a non-exhaustive list of exemplary waveforms that can be used to meet the design requirements.

On the Acquisition of Stationary Signals Using Uniform ADCs

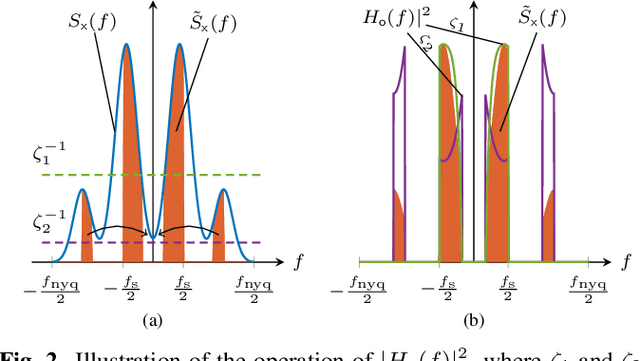
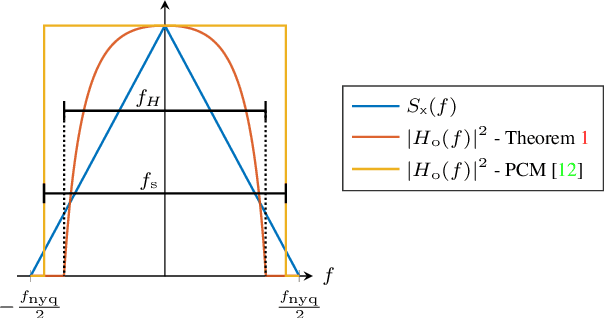
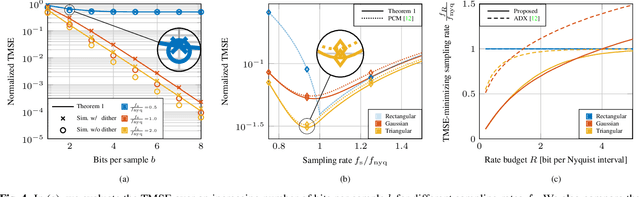
In this work, we consider the acquisition of stationary signals using uniform analog-to-digital converters (ADCs), i.e., employing uniform sampling and scalar uniform quantization. We jointly optimize the pre-sampling and reconstruction filters to minimize the time-averaged mean-squared error (TMSE) in recovering the continuous-time input signal for a fixed sampling rate and quantizer resolution and obtain closed-form expressions for the minimal achievable TMSE. We show that the TMSE-minimizing pre-sampling filter omits aliasing and discards weak frequency components to resolve the remaining ones with higher resolution when the rate budget is small. In our numerical study, we validate our results and show that sub-Nyquist sampling often minimizes the TMSE under tight rate budgets at the output of the ADC.

Testing Optimality of Sequential Decision-Making

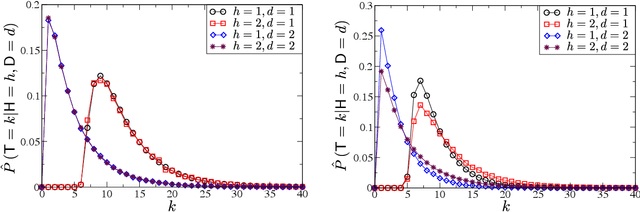
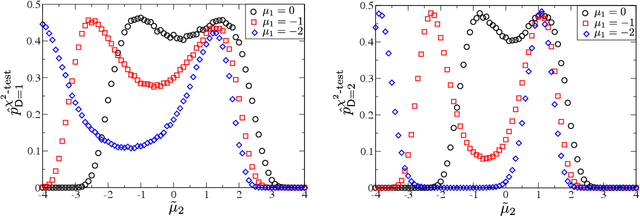
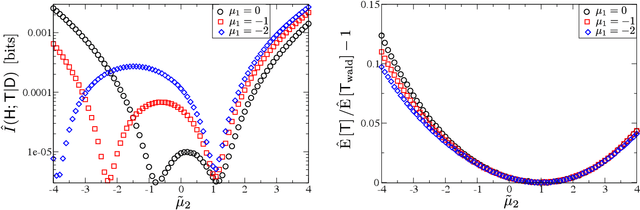
This paper provides a statistical method to test whether a system that performs a binary sequential hypothesis test is optimal in the sense of minimizing the average decision times while taking decisions with given reliabilities. The proposed method requires samples of the decision times, the decision outcomes, and the true hypotheses, but does not require knowledge on the statistics of the observations or the properties of the decision-making system. The method is based on fluctuation relations for decision time distributions which are proved for sequential probability ratio tests. These relations follow from the martingale property of probability ratios and hold under fairly general conditions. We illustrate these tests with numerical experiments and discuss potential applications.