Machine learning for cerebral blood vessels' malformations

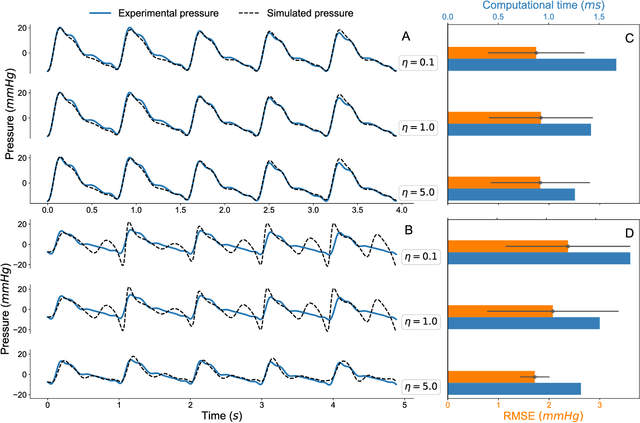
Cerebral aneurysms and arteriovenous malformations are life-threatening hemodynamic pathologies of the brain. While surgical intervention is often essential to prevent fatal outcomes, it carries significant risks both during the procedure and in the postoperative period, making the management of these conditions highly challenging. Parameters of cerebral blood flow, routinely monitored during medical interventions, could potentially be utilized in machine learning-assisted protocols for risk assessment and therapeutic prognosis. To this end, we developed a linear oscillatory model of blood velocity and pressure for clinical data acquired from neurosurgical operations. Using the method of Sparse Identification of Nonlinear Dynamics (SINDy), the parameters of our model can be reconstructed online within milliseconds from a short time series of the hemodynamic variables. The identified parameter values enable automated classification of the blood-flow pathologies by means of logistic regression, achieving an accuracy of 73 %. Our results demonstrate the potential of this model for both diagnostic and prognostic applications, providing a robust and interpretable framework for assessing cerebral blood vessel conditions.

The impact of memory on learning sequence-to-sequence tasks

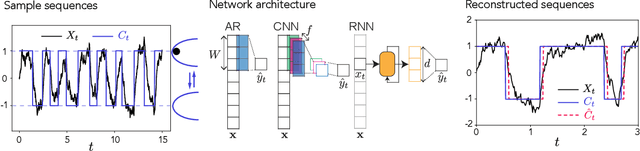
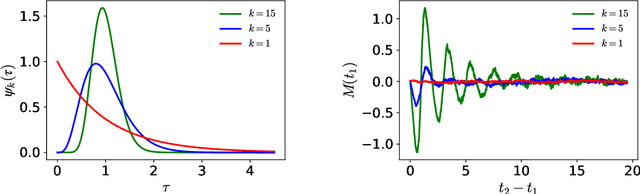
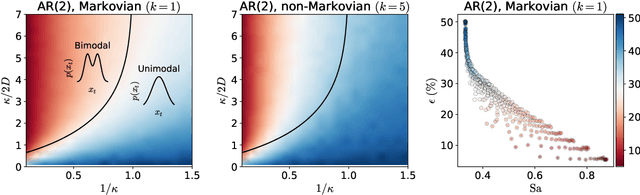
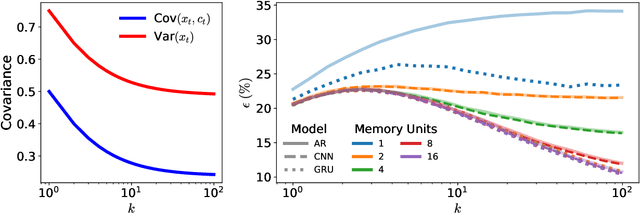
The recent success of neural networks in machine translation and other fields has drawn renewed attention to learning sequence-to-sequence (seq2seq) tasks. While there exists a rich literature that studies classification and regression using solvable models of neural networks, learning seq2seq tasks is significantly less studied from this perspective. Here, we propose a simple model for a seq2seq task that gives us explicit control over the degree of memory, or non-Markovianity, in the sequences -- the stochastic switching-Ornstein-Uhlenbeck (SSOU) model. We introduce a measure of non-Markovianity to quantify the amount of memory in the sequences. For a minimal auto-regressive (AR) learning model trained on this task, we identify two learning regimes corresponding to distinct phases in the stationary state of the SSOU process. These phases emerge from the interplay between two different time scales that govern the sequence statistics. Moreover, we observe that while increasing the memory of the AR model always improves performance, increasing the non-Markovianity of the input sequences can improve or degrade performance. Finally, our experiments with recurrent and convolutional neural networks show that our observations carry over to more complicated neural network architectures.

Testing Optimality of Sequential Decision-Making

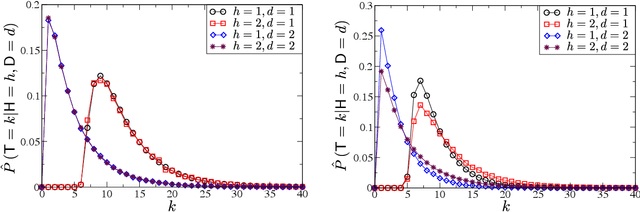
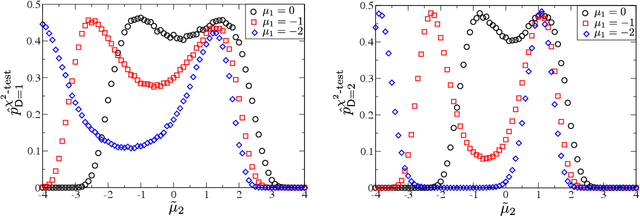
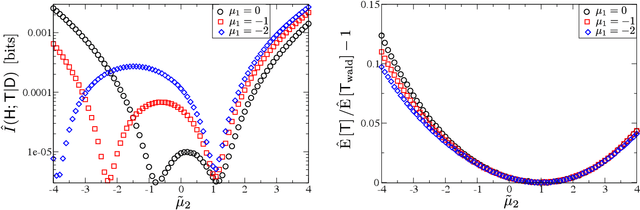
This paper provides a statistical method to test whether a system that performs a binary sequential hypothesis test is optimal in the sense of minimizing the average decision times while taking decisions with given reliabilities. The proposed method requires samples of the decision times, the decision outcomes, and the true hypotheses, but does not require knowledge on the statistics of the observations or the properties of the decision-making system. The method is based on fluctuation relations for decision time distributions which are proved for sequential probability ratio tests. These relations follow from the martingale property of probability ratios and hold under fairly general conditions. We illustrate these tests with numerical experiments and discuss potential applications.