Testing Optimality of Sequential Decision-Making
Paper and Code
Jan 04, 2018
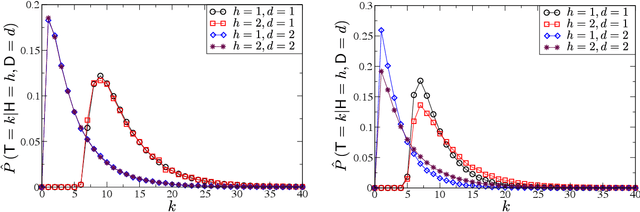
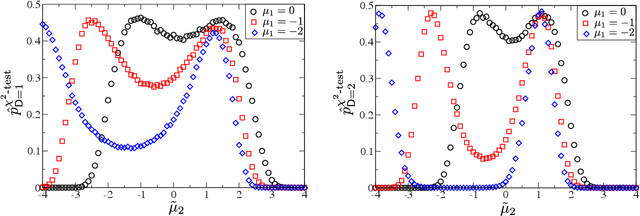
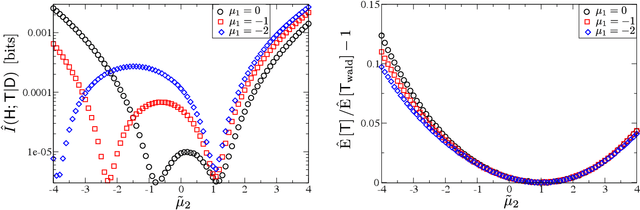
This paper provides a statistical method to test whether a system that performs a binary sequential hypothesis test is optimal in the sense of minimizing the average decision times while taking decisions with given reliabilities. The proposed method requires samples of the decision times, the decision outcomes, and the true hypotheses, but does not require knowledge on the statistics of the observations or the properties of the decision-making system. The method is based on fluctuation relations for decision time distributions which are proved for sequential probability ratio tests. These relations follow from the martingale property of probability ratios and hold under fairly general conditions. We illustrate these tests with numerical experiments and discuss potential applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge