Understanding the Impact of Data Domain Extraction on Synthetic Data Privacy

Privacy attacks, particularly membership inference attacks (MIAs), are widely used to assess the privacy of generative models for tabular synthetic data, including those with Differential Privacy (DP) guarantees. These attacks often exploit outliers, which are especially vulnerable due to their position at the boundaries of the data domain (e.g., at the minimum and maximum values). However, the role of data domain extraction in generative models and its impact on privacy attacks have been overlooked. In this paper, we examine three strategies for defining the data domain: assuming it is externally provided (ideally from public data), extracting it directly from the input data, and extracting it with DP mechanisms. While common in popular implementations and libraries, we show that the second approach breaks end-to-end DP guarantees and leaves models vulnerable. While using a provided domain (if representative) is preferable, extracting it with DP can also defend against popular MIAs, even at high privacy budgets.

The Importance of Being Discrete: Measuring the Impact of Discretization in End-to-End Differentially Private Synthetic Data

Differentially Private (DP) generative marginal models are often used in the wild to release synthetic tabular datasets in lieu of sensitive data while providing formal privacy guarantees. These models approximate low-dimensional marginals or query workloads; crucially, they require the training data to be pre-discretized, i.e., continuous values need to first be partitioned into bins. However, as the range of values (or their domain) is often inferred directly from the training data, with the number of bins and bin edges typically defined arbitrarily, this approach can ultimately break end-to-end DP guarantees and may not always yield optimal utility. In this paper, we present an extensive measurement study of four discretization strategies in the context of DP marginal generative models. More precisely, we design DP versions of three discretizers (uniform, quantile, and k-means) and reimplement the PrivTree algorithm. We find that optimizing both the choice of discretizer and bin count can improve utility, on average, by almost 30% across six DP marginal models, compared to the default strategy and number of bins, with PrivTree being the best-performing discretizer in the majority of cases. We demonstrate that, while DP generative models with non-private discretization remain vulnerable to membership inference attacks, applying DP during discretization effectively mitigates this risk. Finally, we propose an optimized approach for automatically selecting the optimal number of bins, achieving high utility while reducing both privacy budget consumption and computational overhead.

To Shuffle or not to Shuffle: Auditing DP-SGD with Shuffling

Differentially Private Stochastic Gradient Descent (DP-SGD) is a popular method for training machine learning models with formal Differential Privacy (DP) guarantees. As DP-SGD processes the training data in batches, it uses Poisson sub-sampling to select batches at each step. However, due to computational and compatibility benefits, replacing sub-sampling with shuffling has become common practice. Yet, since tight theoretical guarantees for shuffling are currently unknown, prior work using shuffling reports DP guarantees as though Poisson sub-sampling was used. This prompts the need to verify whether this discrepancy is reflected in a gap between the theoretical guarantees from state-of-the-art models and the actual privacy leakage. To do so, we introduce a novel DP auditing procedure to analyze DP-SGD with shuffling. We show that state-of-the-art DP models trained with shuffling appreciably overestimated privacy guarantees (up to 4x). In the process, we assess the impact of several parameters, such as batch size, privacy budget, and threat model, on privacy leakage. Finally, we study two variations of the shuffling procedure found in the wild, which result in further privacy leakage. Overall, our work empirically attests to the risk of using shuffling instead of Poisson sub-sampling vis-\`a-vis the actual privacy leakage of DP-SGD.

It's Our Loss: No Privacy Amplification for Hidden State DP-SGD With Non-Convex Loss

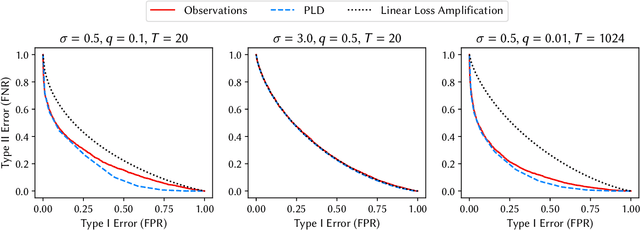
Differentially Private Stochastic Gradient Descent (DP-SGD) is a popular iterative algorithm used to train machine learning models while formally guaranteeing the privacy of users. However the privacy analysis of DP-SGD makes the unrealistic assumption that all intermediate iterates (aka internal state) of the algorithm are released since in practice, only the final trained model, i.e., the final iterate of the algorithm is released. In this hidden state setting, prior work has provided tighter analyses, albeit only when the loss function is constrained, e.g., strongly convex and smooth or linear. On the other hand, the privacy leakage observed empirically from hidden state DP-SGD, even when using non-convex loss functions suggest that there is in fact a gap between the theoretical privacy analysis and the privacy guarantees achieved in practice. Therefore, it remains an open question whether privacy amplification for DP-SGD is possible in the hidden state setting for general loss functions. Unfortunately, this work answers the aforementioned research question negatively. By carefully constructing a loss function for DP-SGD, we show that for specific loss functions, the final iterate of DP-SGD alone leaks as much information as the sequence of all iterates combined. Furthermore, we empirically verify this result by evaluating the privacy leakage from the final iterate of DP-SGD with our loss function and show that this matches the theoretical upper bound guaranteed by DP exactly. Therefore, we show that the current privacy analysis fo DP-SGD is tight for general loss functions and conclude that no privacy amplification is possible for DP-SGD in general for all (possibly non-convex) loss functions.

The Elusive Pursuit of Replicating PATE-GAN: Benchmarking, Auditing, Debugging

Synthetic data created by differentially private (DP) generative models is increasingly used in real-world settings. In this context, PATE-GAN has emerged as a popular algorithm, combining Generative Adversarial Networks (GANs) with the private training approach of PATE (Private Aggregation of Teacher Ensembles). In this paper, we analyze and benchmark six open-source PATE-GAN implementations, including three by (a subset of) the original authors. First, we shed light on architecture deviations and empirically demonstrate that none replicate the utility performance reported in the original paper. Then, we present an in-depth privacy evaluation, including DP auditing, showing that all implementations leak more privacy than intended and uncovering 17 privacy violations and 5 other bugs. Our codebase is available from https://github.com/spalabucr/pategan-audit.

Nearly Tight Black-Box Auditing of Differentially Private Machine Learning

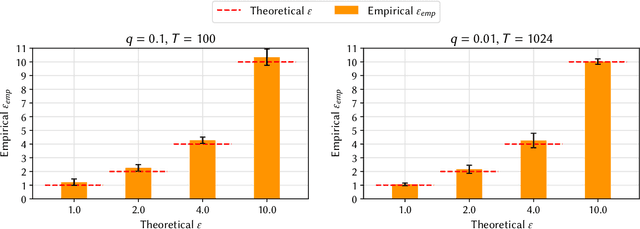
This paper presents a nearly tight audit of the Differentially Private Stochastic Gradient Descent (DP-SGD) algorithm in the black-box model. Our auditing procedure empirically estimates the privacy leakage from DP-SGD using membership inference attacks; unlike prior work, the estimates are appreciably close to the theoretical DP bounds. The main intuition is to craft worst-case initial model parameters, as DP-SGD's privacy analysis is agnostic to the choice of the initial model parameters. For models trained with theoretical $\varepsilon=10.0$ on MNIST and CIFAR-10, our auditing procedure yields empirical estimates of $7.21$ and $6.95$, respectively, on 1,000-record samples and $6.48$ and $4.96$ on the full datasets. By contrast, previous work achieved tight audits only in stronger (i.e., less realistic) white-box models that allow the adversary to access the model's inner parameters and insert arbitrary gradients. Our auditing procedure can be used to detect bugs and DP violations more easily and offers valuable insight into how the privacy analysis of DP-SGD can be further improved.

A Linear Reconstruction Approach for Attribute Inference Attacks against Synthetic Data

Personal data collected at scale from surveys or digital devices offers important insights for statistical analysis and scientific research. Safely sharing such data while protecting privacy is however challenging. Anonymization allows data to be shared while minimizing privacy risks, but traditional anonymization techniques have been repeatedly shown to provide limited protection against re-identification attacks in practice. Among modern anonymization techniques, synthetic data generation (SDG) has emerged as a potential solution to find a good tradeoff between privacy and statistical utility. Synthetic data is typically generated using algorithms that learn the statistical distribution of the original records, to then generate "artificial" records that are structurally and statistically similar to the original ones. Yet, the fact that synthetic records are "artificial" does not, per se, guarantee that privacy is protected. In this work, we systematically evaluate the tradeoffs between protecting privacy and preserving statistical utility for a wide range of synthetic data generation algorithms. Modeling privacy as protection against attribute inference attacks (AIAs), we extend and adapt linear reconstruction attacks, which have not been previously studied in the context of synthetic data. While prior work suggests that AIAs may be effective only on few outlier records, we show they can be very effective even on randomly selected records. We evaluate attacks on synthetic datasets ranging from 10^3 to 10^6 records, showing that even for the same generative model, the attack effectiveness can drastically increase when a larger number of synthetic records is generated. Overall, our findings prove that synthetic data is subject to privacy-utility tradeoffs just like other anonymization techniques: when good utility is preserved, attribute inference can be a risk for many data subjects.