LLM Guided Inductive Inference for Solving Compositional Problems

While large language models (LLMs) have demonstrated impressive performance in question-answering tasks, their performance is limited when the questions require knowledge that is not included in the model's training data and can only be acquired through direct observation or interaction with the real world. Existing methods decompose reasoning tasks through the use of modules invoked sequentially, limiting their ability to answer deep reasoning tasks. We introduce a method, Recursion based extensible LLM (REBEL), which handles open-world, deep reasoning tasks by employing automated reasoning techniques like dynamic planning and forward-chaining strategies. REBEL allows LLMs to reason via recursive problem decomposition and utilization of external tools. The tools that REBEL uses are specified only by natural language description. We further demonstrate REBEL capabilities on a set of problems that require a deeply nested use of external tools in a compositional and conversational setting.

The Fundamental Limits of Interval Arithmetic for Neural Networks

Interval analysis (or interval bound propagation, IBP) is a popular technique for verifying and training provably robust deep neural networks, a fundamental challenge in the area of reliable machine learning. However, despite substantial efforts, progress on addressing this key challenge has stagnated, calling into question whether interval arithmetic is a viable path forward. In this paper we present two fundamental results on the limitations of interval arithmetic for analyzing neural networks. Our main impossibility theorem states that for any neural network classifying just three points, there is a valid specification over these points that interval analysis can not prove. Further, in the restricted case of one-hidden-layer neural networks we show a stronger impossibility result: given any radius $\alpha < 1$, there is a set of $O(\alpha^{-1})$ points with robust radius $\alpha$, separated by distance $2$, that no one-hidden-layer network can be proven to classify robustly via interval analysis.

Robustness Certification of Generative Models

Generative neural networks can be used to specify continuous transformations between images via latent-space interpolation. However, certifying that all images captured by the resulting path in the image manifold satisfy a given property can be very challenging. This is because this set is highly non-convex, thwarting existing scalable robustness analysis methods, which are often based on convex relaxations. We present ApproxLine, a scalable certification method that successfully verifies non-trivial specifications involving generative models and classifiers. ApproxLine can provide both sound deterministic and probabilistic guarantees, by capturing either infinite non-convex sets of neural network activation vectors or distributions over such sets. We show that ApproxLine is practically useful and can verify interesting interpolations in the networks latent space.

Online Robustness Training for Deep Reinforcement Learning

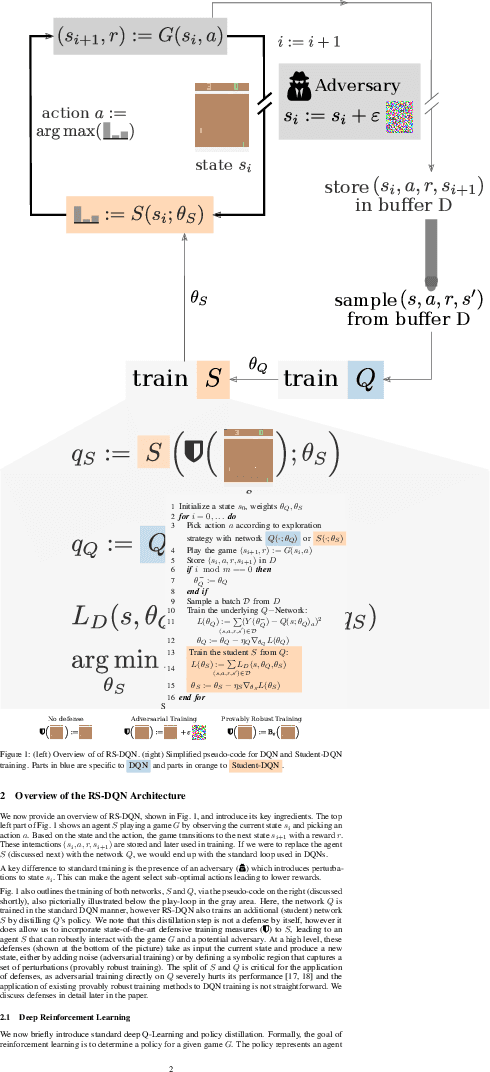
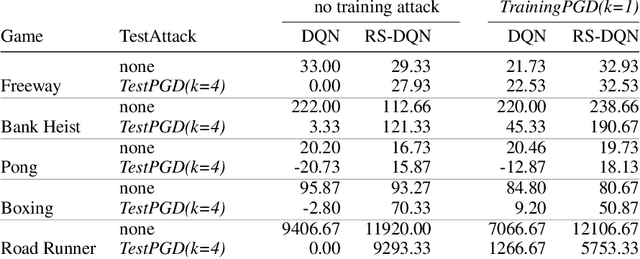
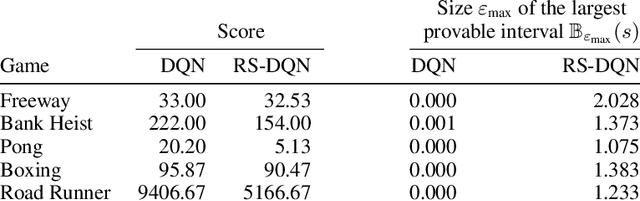
In deep reinforcement learning (RL), adversarial attacks can trick an agent into unwanted states and disrupt training. We propose a system called Robust Student-DQN (RS-DQN), which permits online robustness training alongside Q networks, while preserving competitive performance. We show that RS-DQN can be combined with (i) state-of-the-art adversarial training and (ii) provably robust training to obtain an agent that is resilient to strong attacks during training and evaluation.

Universal Approximation with Certified Networks

Training neural networks to be certifiably robust is a powerful defense against adversarial attacks. However, while promising, state-of-the-art results with certified training are far from satisfactory. Currently, it is very difficult to train a neural network that is both accurate and certified on realistic datasets and specifications (e.g., robustness). Given this difficulty, a pressing existential question is: given a dataset and a specification, is there a network that is both certified and accurate with respect to these? While the evidence suggests "no", we prove that for realistic datasets and specifications, such a network does exist and its certification can be established by propagating lower and upper bounds of each neuron through the network (interval analysis) - the most relaxed yet computationally efficient convex relaxation. Our result can be seen as a Universal Approximation Theorem for interval-certified ReLU networks. To the best of our knowledge, this is the first work to prove the existence of accurate, interval-certified networks.

A Provable Defense for Deep Residual Networks

We present a training system, which can provably defend significantly larger neural networks than previously possible, including ResNet-34 and DenseNet-100. Our approach is based on differentiable abstract interpretation and introduces two novel concepts: (i) abstract layers for fine-tuning the precision and scalability of the abstraction, (ii) a flexible domain specific language (DSL) for describing training objectives that combine abstract and concrete losses with arbitrary specifications. Our training method is implemented in the DiffAI system.