Wasserstein Weisfeiler-Lehman Graph Kernels

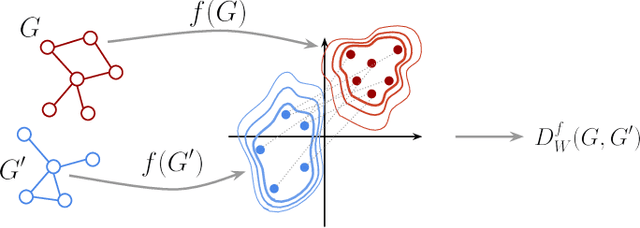
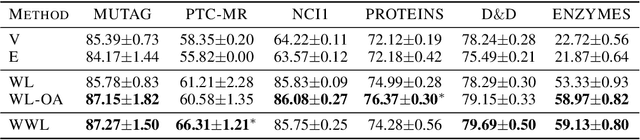
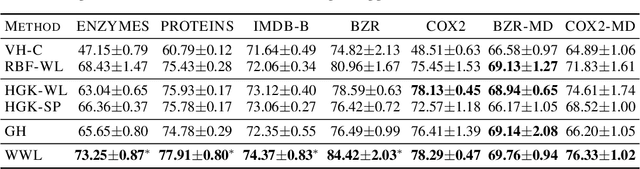
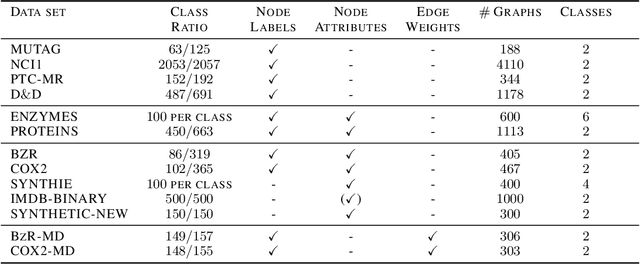
Graph kernels are an instance of the class of $\mathcal{R}$-Convolution kernels, which measure the similarity of objects by comparing their substructures. Despite their empirical success, most graph kernels use a naive aggregation of the final set of substructures, usually a sum or average, thereby potentially discarding valuable information about the distribution of individual components. Furthermore, only a limited instance of these approaches can be extended to continuously attributed graphs. We propose a novel method that relies on the Wasserstein distance between the node feature vector distributions of two graphs, which allows to find subtler differences in data sets by considering graphs as high-dimensional objects, rather than simple means. We further propose a Weisfeiler-Lehman inspired embedding scheme for graphs with continuous node attributes and weighted edges, enhance it with the computed Wasserstein distance, and thus improve the state-of-the-art prediction performance on several graph classification tasks.

Neural Persistence: A Complexity Measure for Deep Neural Networks Using Algebraic Topology

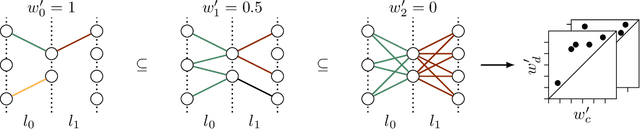
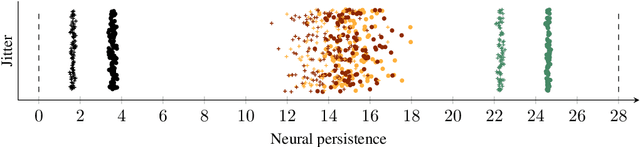
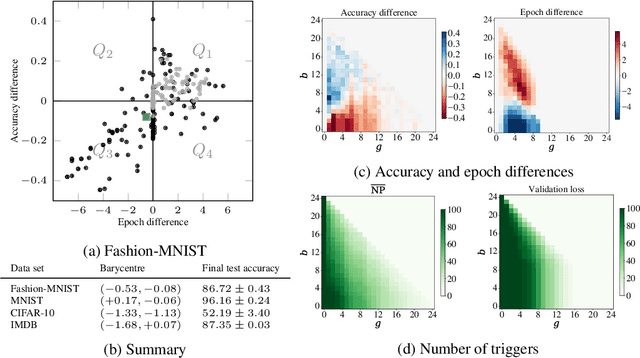
While many approaches to make neural networks more fathomable have been proposed, they are restricted to interrogating the network with input data. Measures for characterizing and monitoring structural properties, however, have not been developed. In this work, we propose neural persistence, a complexity measure for neural network architectures based on topological data analysis on weighted stratified graphs. To demonstrate the usefulness of our approach, we show that neural persistence reflects best practices developed in the deep learning community such as dropout and batch normalization. Moreover, we derive a neural persistence-based stopping criterion that shortens the training process while achieving comparable accuracies as early stopping based on validation loss.