Deontic Meta-Rules

The use of meta-rules in logic, i.e., rules whose content includes other rules, has recently gained attention in the setting of non-monotonic reasoning: a first logical formalisation and efficient algorithms to compute the (meta)-extensions of such theories were proposed in Olivieri et al (2021) This work extends such a logical framework by considering the deontic aspect. The resulting logic will not just be able to model policies but also tackle well-known aspects that occur in numerous legal systems. The use of Defeasible Logic (DL) to model meta-rules in the application area we just alluded to has been investigated. Within this line of research, the study mentioned above was not focusing on the general computational properties of meta-rules. This study fills this gap with two major contributions. First, we introduce and formalise two variants of Defeasible Deontic Logic with Meta-Rules to represent (1) defeasible meta-theories with deontic modalities, and (2) two different types of conflicts among rules: Simple Conflict Defeasible Deontic Logic, and Cautious Conflict Defeasible Deontic Logic. Second, we advance efficient algorithms to compute the extensions for both variants.

Applications of Linear Defeasible Logic: combining resource consumption and exceptions to energy management and business processes

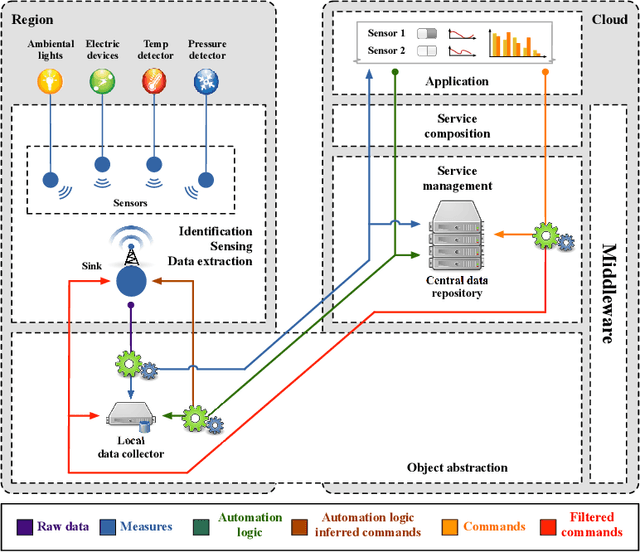
Linear Logic and Defeasible Logic have been adopted to formalise different features of knowledge representation: consumption of resources, and non monotonic reasoning in particular to represent exceptions. Recently, a framework to combine sub-structural features, corresponding to the consumption of resources, with defeasibility aspects to handle potentially conflicting information, has been discussed in literature, by some of the authors. Two applications emerged that are very relevant: energy management and business process management. We illustrate a set of guide lines to determine how to apply linear defeasible logic to those contexts.

It could be worse, it could be raining: reliable automatic meteorological forecasting

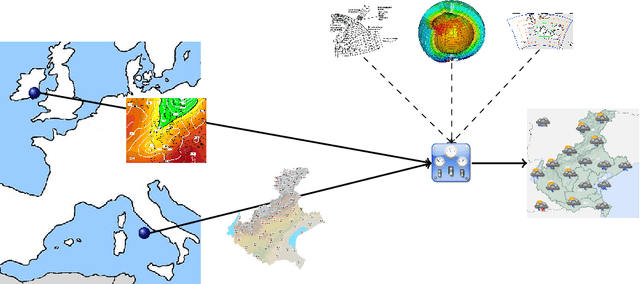
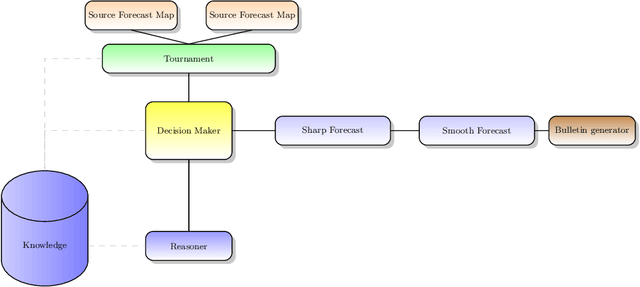
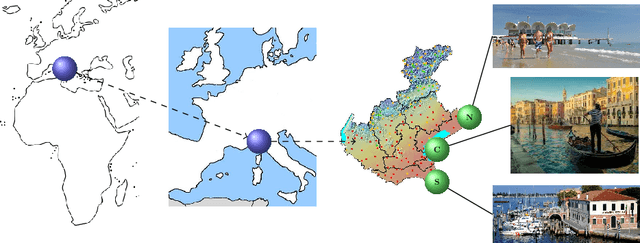
Meteorological forecasting provides reliable prediction about the future weather within a given interval of time. Meteorological forecasting can be viewed as a form of hybrid diagnostic reasoning and can be mapped onto an integrated conceptual framework. The automation of the forecasting process would be helpful in a number of contexts, in particular: when the amount of data is too wide to be dealt with manually; to support forecasters education; when forecasting about underpopulated geographic areas is not interesting for everyday life (and then is out from human forecasters' tasks) but is central for tourism sponsorship. We present logic MeteoLOG, a framework that models the main steps of the reasoner the forecaster adopts to provide a bulletin. MeteoLOG rests on several traditions, mainly on fuzzy, temporal and probabilistic logics. On this basis, we also introduce the algorithm Tournament, that transforms a set of MeteoLOG rules into a defeasible theory, that can be implemented into an automatic reasoner. We finally propose an example that models a real world forecasting scenario.

Resource-driven Substructural Defeasible Logic

Linear Logic and Defeasible Logic have been adopted to formalise different features relevant to agents: consumption of resources, and reasoning with exceptions. We propose a framework to combine sub-structural features, corresponding to the consumption of resources, with defeasibility aspects, and we discuss the design choices for the framework.

The Rationale behind the Concept of Goal

The paper proposes a fresh look at the concept of goal and advances that motivational attitudes like desire, goal and intention are just facets of the broader notion of (acceptable) outcome. We propose to encode the preferences of an agent as sequences of "alternative acceptable outcomes". We then study how the agent's beliefs and norms can be used to filter the mental attitudes out of the sequences of alternative acceptable outcomes. Finally, we formalise such intuitions in a novel Modal Defeasible Logic and we prove that the resulting formalisation is computationally feasible.

Strategic Argumentation is NP-Complete

In this paper we study the complexity of strategic argumentation for dialogue games. A dialogue game is a 2-player game where the parties play arguments. We show how to model dialogue games in a skeptical, non-monotonic formalism, and we show that the problem of deciding what move (set of rules) to play at each turn is an NP-complete problem.

Revision of Defeasible Logic Preferences

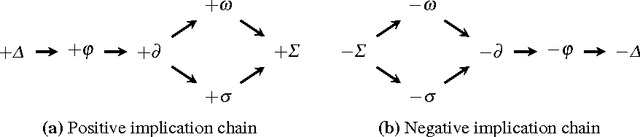
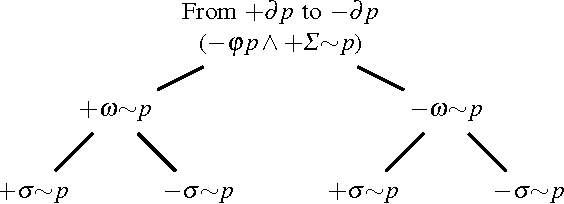
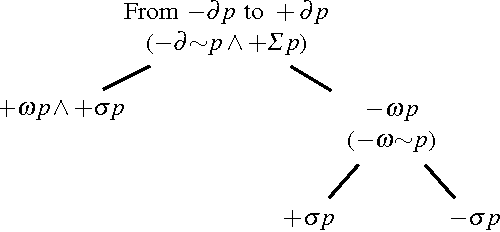
There are several contexts of non-monotonic reasoning where a priority between rules is established whose purpose is preventing conflicts. One formalism that has been widely employed for non-monotonic reasoning is the sceptical one known as Defeasible Logic. In Defeasible Logic the tool used for conflict resolution is a preference relation between rules, that establishes the priority among them. In this paper we investigate how to modify such a preference relation in a defeasible logic theory in order to change the conclusions of the theory itself. We argue that the approach we adopt is applicable to legal reasoning where users, in general, cannot change facts or rules, but can propose their preferences about the relative strength of the rules. We provide a comprehensive study of the possible combinatorial cases and we identify and analyse the cases where the revision process is successful. After this analysis, we identify three revision/update operators and study them against the AGM postulates for belief revision operators, to discover that only a part of these postulates are satisfied by the three operators.

Meaning Negotiation as Inference

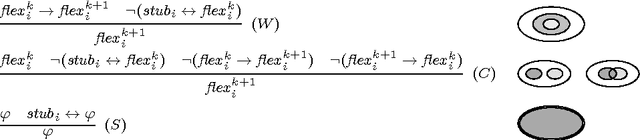
Meaning negotiation (MN) is the general process with which agents reach an agreement about the meaning of a set of terms. Artificial Intelligence scholars have dealt with the problem of MN by means of argumentations schemes, beliefs merging and information fusion operators, and ontology alignment but the proposed approaches depend upon the number of participants. In this paper, we give a general model of MN for an arbitrary number of agents, in which each participant discusses with the others her viewpoint by exhibiting it in an actual set of constraints on the meaning of the negotiated terms. We call this presentation of individual viewpoints an angle. The agents do not aim at forming a common viewpoint but, instead, at agreeing about an acceptable common angle. We analyze separately the process of MN by two agents (\emph{bilateral} or \emph{pairwise} MN) and by more than two agents (\emph{multiparty} MN), and we use game theoretic models to understand how the process develops in both cases: the models are Bargaining Game for bilateral MN and English Auction for multiparty MN. We formalize the process of reaching such an agreement by giving a deduction system that comprises of rules that are consistent and adequate for representing MN.