The Rationale behind the Concept of Goal

The paper proposes a fresh look at the concept of goal and advances that motivational attitudes like desire, goal and intention are just facets of the broader notion of (acceptable) outcome. We propose to encode the preferences of an agent as sequences of "alternative acceptable outcomes". We then study how the agent's beliefs and norms can be used to filter the mental attitudes out of the sequences of alternative acceptable outcomes. Finally, we formalise such intuitions in a novel Modal Defeasible Logic and we prove that the resulting formalisation is computationally feasible.

Strategic Argumentation is NP-Complete

In this paper we study the complexity of strategic argumentation for dialogue games. A dialogue game is a 2-player game where the parties play arguments. We show how to model dialogue games in a skeptical, non-monotonic formalism, and we show that the problem of deciding what move (set of rules) to play at each turn is an NP-complete problem.

Computing Strong and Weak Permissions in Defeasible Logic

In this paper we propose an extension of Defeasible Logic to represent and compute three concepts of defeasible permission. In particular, we discuss different types of explicit permissive norms that work as exceptions to opposite obligations. Moreover, we show how strong permissions can be represented both with, and without introducing a new consequence relation for inferring conclusions from explicit permissive norms. Finally, we illustrate how a preference operator applicable to contrary-to-duty obligations can be combined with a new operator representing ordered sequences of strong permissions which derogate from prohibitions. The logical system is studied from a computational standpoint and is shown to have liner computational complexity.

Revision of Defeasible Logic Preferences

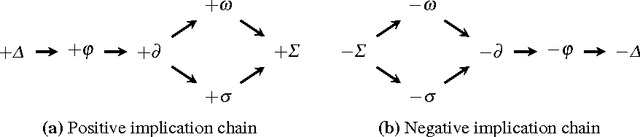
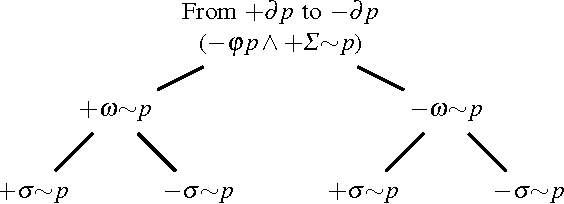
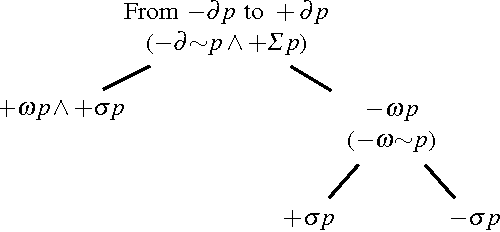
There are several contexts of non-monotonic reasoning where a priority between rules is established whose purpose is preventing conflicts. One formalism that has been widely employed for non-monotonic reasoning is the sceptical one known as Defeasible Logic. In Defeasible Logic the tool used for conflict resolution is a preference relation between rules, that establishes the priority among them. In this paper we investigate how to modify such a preference relation in a defeasible logic theory in order to change the conclusions of the theory itself. We argue that the approach we adopt is applicable to legal reasoning where users, in general, cannot change facts or rules, but can propose their preferences about the relative strength of the rules. We provide a comprehensive study of the possible combinatorial cases and we identify and analyse the cases where the revision process is successful. After this analysis, we identify three revision/update operators and study them against the AGM postulates for belief revision operators, to discover that only a part of these postulates are satisfied by the three operators.