Convergence of Momentum-Based Optimization Algorithms with Time-Varying Parameters

In this paper, we present a unified algorithm for stochastic optimization that makes use of a "momentum" term; in other words, the stochastic gradient depends not only on the current true gradient of the objective function, but also on the true gradient at the previous iteration. Our formulation includes the Stochastic Heavy Ball (SHB) and the Stochastic Nesterov Accelerated Gradient (SNAG) algorithms as special cases. In addition, in our formulation, the momentum term is allowed to vary as a function of time (i.e., the iteration counter). The assumptions on the stochastic gradient are the most general in the literature, in that it can be biased, and have a conditional variance that grows in an unbounded fashion as a function of time. This last feature is crucial in order to make the theory applicable to "zero-order" methods, where the gradient is estimated using just two function evaluations. We present a set of sufficient conditions for the convergence of the unified algorithm. These conditions are natural generalizations of the familiar Robbins-Monro and Kiefer-Wolfowitz-Blum conditions for standard stochastic gradient descent. We also analyze another method from the literature for the SHB algorithm with a time-varying momentum parameter, and show that it is impracticable.

Revisiting Stochastic Approximation and Stochastic Gradient Descent

In this paper, we take a fresh look at stochastic approximation (SA) and Stochastic Gradient Descent (SGD). We derive new sufficient conditions for the convergence of SA. In particular, the "noise" or measurement error need not have a finite second moment, and under suitable conditions, not even a finite mean. By adapting this method of proof, we also derive sufficient conditions for the convergence of zero-order SGD, wherein the stochastic gradient is computed using only two function evaluations, and no gradient computations. The sufficient conditions derived here are the weakest to date, thus leading to a considerable expansion of the applicability of SA and SGD theory.

A Tutorial Introduction to Reinforcement Learning

In this paper, we present a brief survey of Reinforcement Learning (RL), with particular emphasis on Stochastic Approximation (SA) as a unifying theme. The scope of the paper includes Markov Reward Processes, Markov Decision Processes, Stochastic Approximation algorithms, and widely used algorithms such as Temporal Difference Learning and $Q$-learning.

Convergence of Momentum-Based Heavy Ball Method with Batch Updating and/or Approximate Gradients

In this paper, we study the well-known "Heavy Ball" method for convex and nonconvex optimization introduced by Polyak in 1964, and establish its convergence under a variety of situations. Traditionally, most algorthms use "full-coordinate update," that is, at each step, very component of the argument is updated. However, when the dimension of the argument is very high, it is more efficient to update some but not all components of the argument at each iteration. We refer to this as "batch updating" in this paper. When gradient-based algorithms are used together with batch updating, in principle it is sufficient to compute only those components of the gradient for which the argument is to be updated. However, if a method such as back propagation is used to compute these components, computing only some components of gradient does not offer much savings over computing the entire gradient. Therefore, to achieve a noticeable reduction in CPU usage at each step, one can use first-order differences to approximate the gradient. The resulting estimates are biased, and also have unbounded variance. Thus some delicate analysis is required to ensure that the HB algorithm converge when batch updating is used instead of full-coordinate updating, and/or approximate gradients are used instead of true gradients. In this paper, we not only establish the almost sure convergence of the iterations to the stationary point(s) of the objective function, but also derive upper bounds on the rate of convergence. To the best of our knowledge, there is no other paper that combines all of these features.

Estimating large causal polytree skeletons from small samples

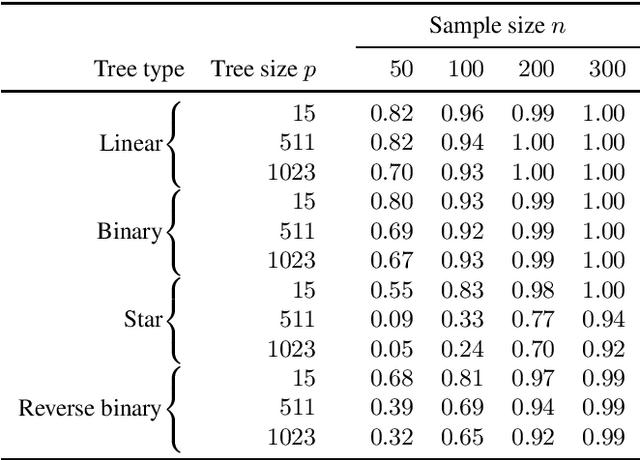
We consider the problem of estimating the skeleton of a large causal polytree from a relatively small i.i.d. sample. This is motivated by the problem of determining causal structure when the number of variables is very large compared to the sample size, such as in gene regulatory networks. We give an algorithm that recovers the tree with high accuracy in such settings. The algorithm works under essentially no distributional or modeling assumptions other than some mild non-degeneracy conditions.

Deterministic Completion of Rectangular Matrices Using Ramanujan Bigraphs -- II: Explicit Constructions and Phase Transitions

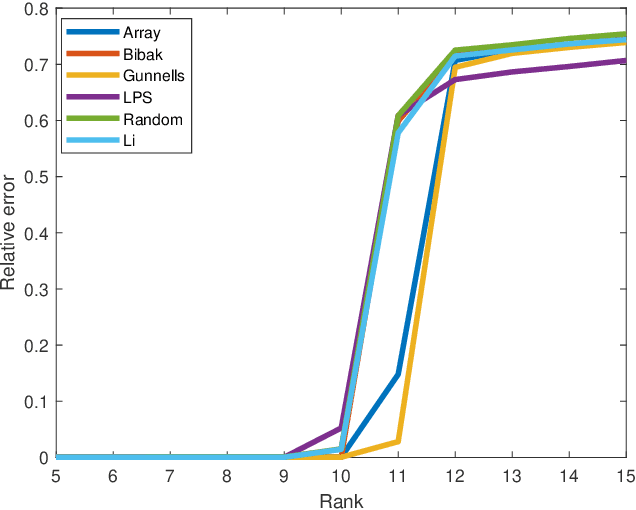
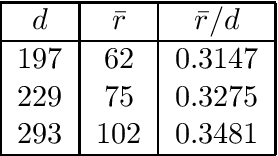
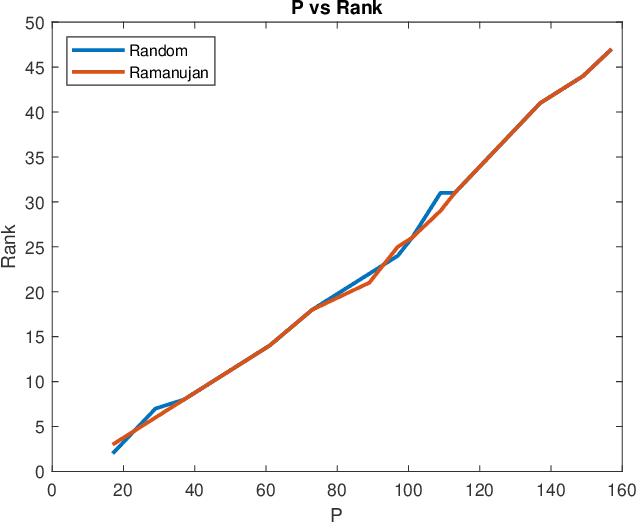
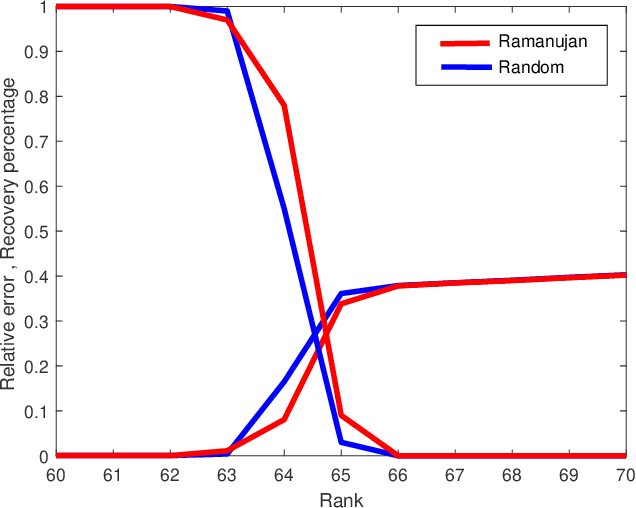
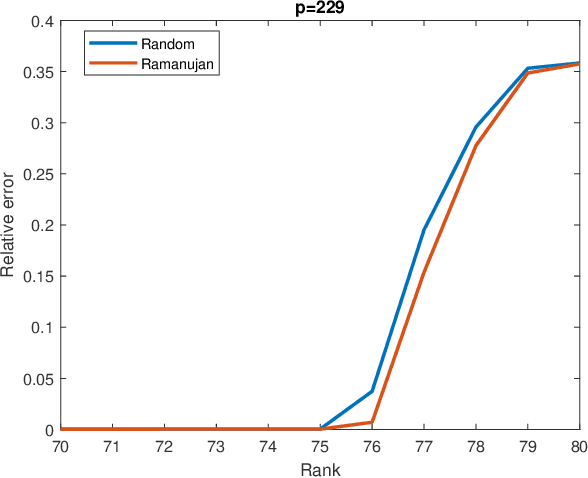
Matrix completion is a part of compressed sensing, and refers to determining an unknown low-rank matrix from a relatively small number of samples of the elements of the matrix. The problem has applications in recommendation engines, sensor localization, quantum tomography etc. In a companion paper (Part-1), the first and second author showed that it is possible to guarantee exact completion of an unknown low rank matrix, if the sample set corresponds to the edge set of a Ramanujan bigraph. In this paper, we present for the first time an infinite family of unbalanced Ramanujan bigraphs with explicitly constructed biadjacency matrices. In addition, we also show how to construct the adjacency matrices for the currently available families of Ramanujan graphs. In an attempt to determine how close the sufficient condition presented in Part-1 is to being necessary, we carried out numerical simulations of nuclear norm minimization on randomly generated low-rank matrices. The results revealed several noteworthy points, the most interesting of which is the existence of a phase transition. For square matrices, the maximum rank $\bar{r}$ for which nuclear norm minimization correctly completes all low-rank matrices is approximately $\bar{r} \approx d/3$, where $d$ is the degree of the Ramanujan graph. This upper limit appears to be independent of the specific family of Ramanujan graphs. The percentage of low-rank matrices that are recovered changes from 100% to 0% if the rank is increased by just two beyond $\bar{r}$. Again, this phenomenon appears to be independent of the specific family of Ramanujan graphs.

Deterministic Completion of Rectangular Matrices Using Asymmetric Ramanujan Graphs

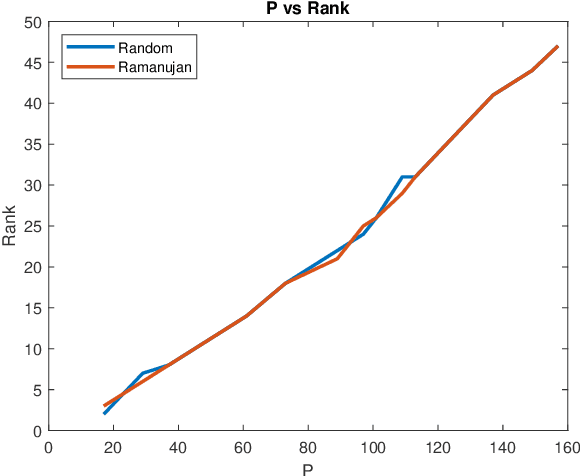
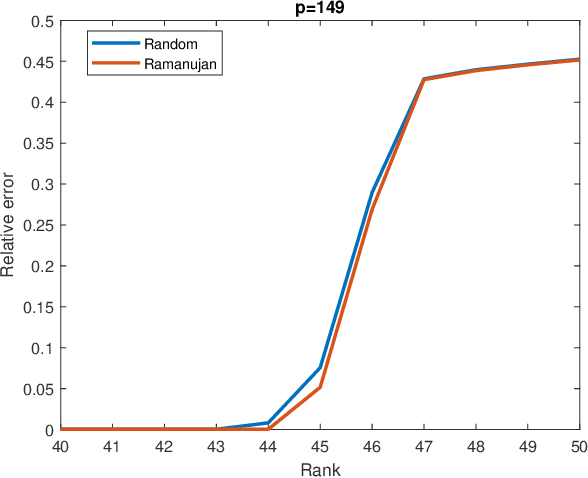
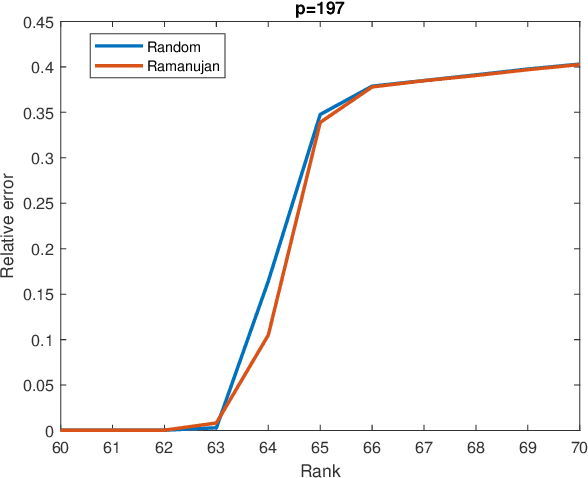
In this paper we study the matrix completion problem: Suppose $X \in \mathbb{R}^{n_r \times n_c}$ is unknown except for an upper bound $r$ on its rank. By measuring a small number $m \ll n_r n_c$ of elements of $X$, is it possible to recover $X$ exactly, or at least, to construct a reasonable approximation of $X$? There are two approaches to choosing the sample set, namely probabilistic and deterministic. At present there are very few deterministic methods, and they apply only to square matrices. The focus in the present paper is on deterministic methods that work for rectangular as well as square matrices. The elements to be sampled are chosen as the edge set of an asymmetric Ramanujan graph. For such a measurement matrix, we derive bounds on the error between a scaled version of the sampled matrix and unknown matrix, and show that, under suitable conditions, the unknown matrix can be recovered exactly. Even for the case of square matrices, these bounds are an improvement on known results. Of course they are entirely new for rectangular matrices. This raises the question of how such asymmetric Ramanujan graphs might be constructed. While some techniques exist for constructing Ramanujan bipartite graphs with equal numbers of vertices on both sides, until now no methods exist for constructing Ramanujan bipartite graphs with unequal numbers of vertices on the two sides. We provide a method for the construction of an infinite family of asymmetric biregular Ramanujan graphs with $q^2$ left vertices and $lq$ right vertices, where $q$ is any prime number and $l$ is any integer between $2$ and $q$. The left degree is $l$ and the right degree is $q$. So far as the authors are aware, this is the first explicit construction of an infinite family of asymmetric Ramanujan graphs.

Compressed Sensing Using Binary Matrices of Nearly Optimal Dimensions

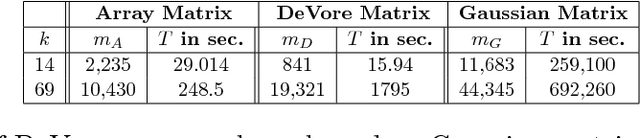
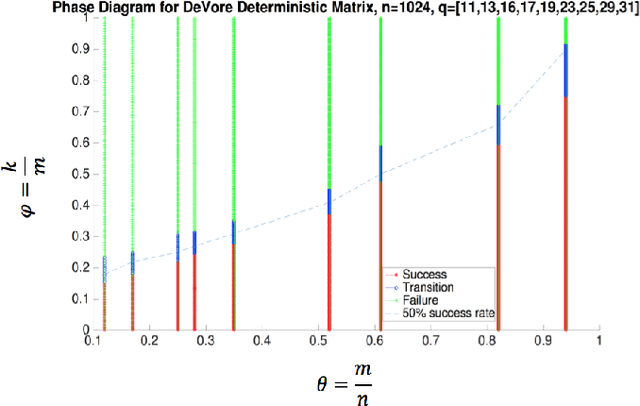
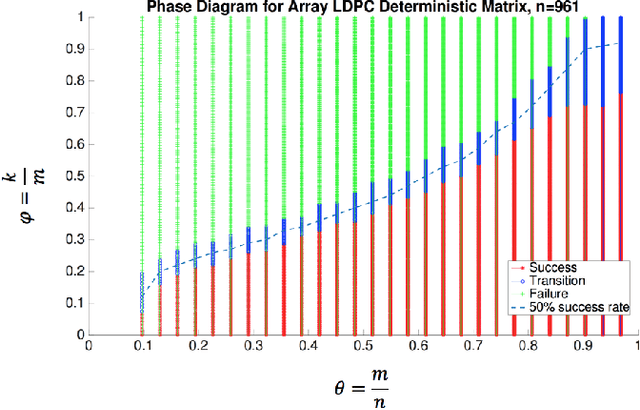
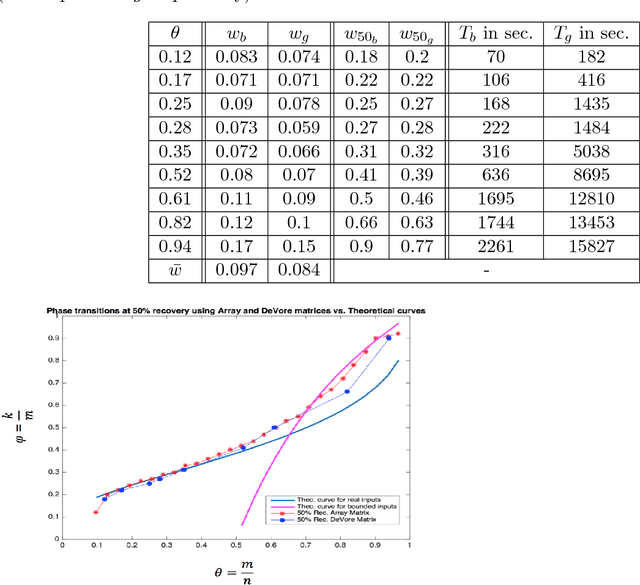
In this paper, we study the problem of compressed sensing using binary measurement matrices, and $\ell_1$-norm minimization (basis pursuit) as the recovery algorithm. We derive new upper and lower bounds on the number of measurements to achieve robust sparse recovery with binary matrices. We establish sufficient conditions for a column-regular binary matrix to satisfy the robust null space property (RNSP), and show that the sparsity bounds for robust sparse recovery obtained using the RNSP are better by a factor of $(3 \sqrt{3})/2 \approx 2.6$ compared to the restricted isometry property (RIP). Next we derive universal \textit{lower} bounds on the number of measurements that any binary matrix needs to have in order to satisfy the weaker sufficient condition based on the RNSP, and show that bipartite graphs of girth six are optimal. Then we display two classes of binary matrices, namely parity check matrices of array codes, and Euler squares, that have girth six and are nearly optimal in the sense of almost satisfying the lower bound. In principle randomly generated Gaussian measurement matrices are `order-optimal.' So we compare the phase transition behavior of the basis pursuit formulation using binary array code and Gaussian matrices, and show that (i) there is essentially no difference between the phase transition boundaries in the two cases, and (ii) the CPU time of basis pursuit with binary matrices is hundreds of times faster than with Gaussian matrices, and the storage requirements are less. Therefore it is suggested that binary matrices are a viable alternative to Gaussian matrices for compressed sensing using basis pursuit.

Tight Performance Bounds for Compressed Sensing With Conventional and Group Sparsity

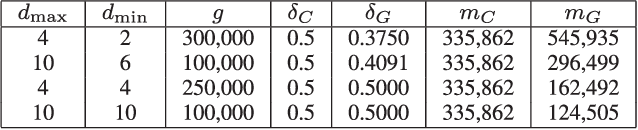
In this paper, we study the problem of recovering a group sparse vector from a small number of linear measurements. In the past the common approach has been to use various "group sparsity-inducing" norms such as the Group LASSO norm for this purpose. By using the theory of convex relaxations, we show that it is also possible to use $\ell_1$-norm minimization for group sparse recovery. We introduce a new concept called group robust null space property (GRNSP), and show that, under suitable conditions, a group version of the restricted isometry property (GRIP) implies the GRNSP, and thus leads to group sparse recovery. When all groups are of equal size, our bounds are less conservative than known bounds. Moreover, our results apply even to situations where where the groups have different sizes. When specialized to conventional sparsity, our bounds reduce to one of the well-known "best possible" conditions for sparse recovery. This relationship between GRNSP and GRIP is new even for conventional sparsity, and substantially streamlines the proofs of some known results. Using this relationship, we derive bounds on the $\ell_p$-norm of the residual error vector for all $p \in [1,2]$, and not just when $p = 2$. When the measurement matrix consists of random samples of a sub-Gaussian random variable, we present bounds on the number of measurements, which are less conservative than currently known bounds.

A Fast Noniterative Algorithm for Compressive Sensing Using Binary Measurement Matrices

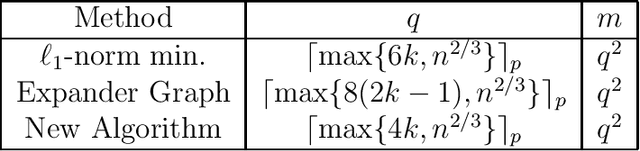
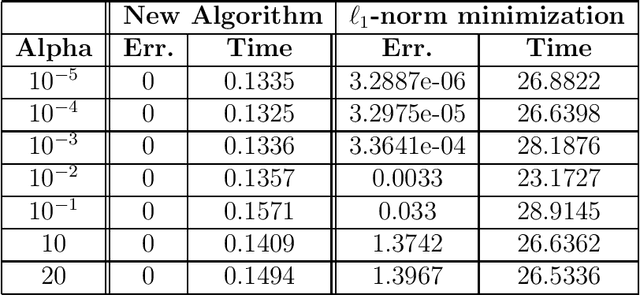
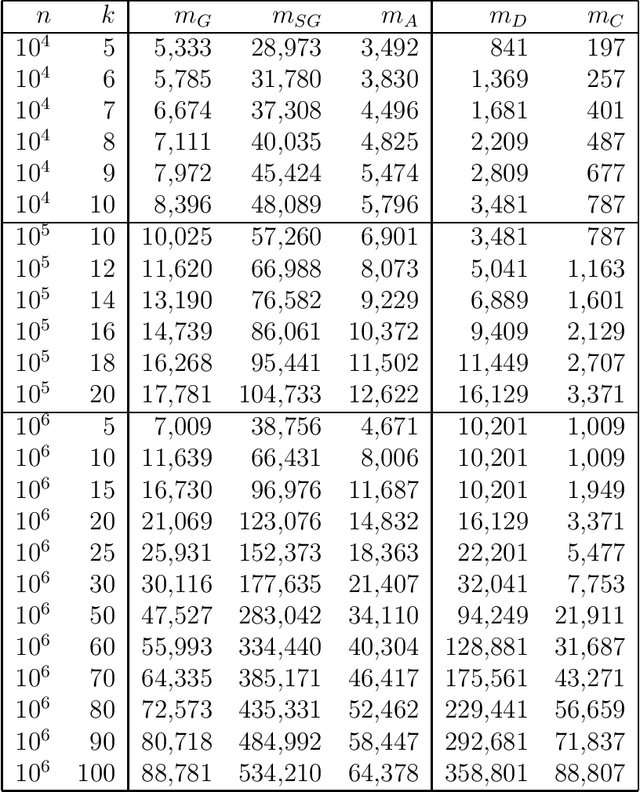
In this paper we present a new algorithm for compressive sensing that makes use of binary measurement matrices and achieves exact recovery of ultra sparse vectors, in a single pass and without any iterations. Due to its noniterative nature, our algorithm is hundreds of times faster than $\ell_1$-norm minimization, and methods based on expander graphs, both of which require multiple iterations. Our algorithm can accommodate nearly sparse vectors, in which case it recovers index set of the largest components, and can also accommodate burst noise measurements. Compared to compressive sensing methods that are guaranteed to achieve exact recovery of all sparse vectors, our method requires fewer measurements However, methods that achieve statistical recovery, that is, recovery of almost all but not all sparse vectors, can require fewer measurements than our method.