Deterministic Completion of Rectangular Matrices Using Ramanujan Bigraphs -- II: Explicit Constructions and Phase Transitions

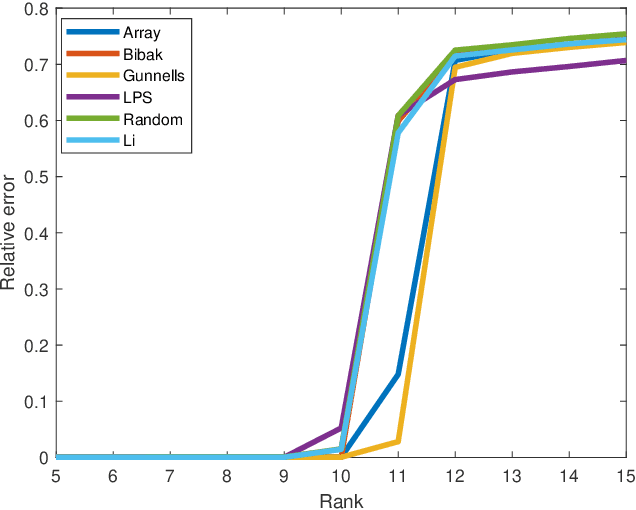
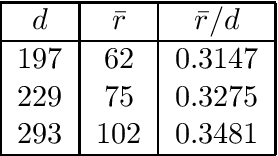
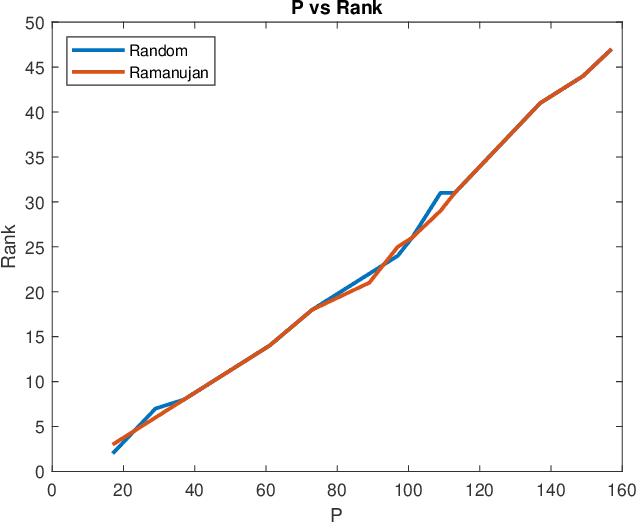
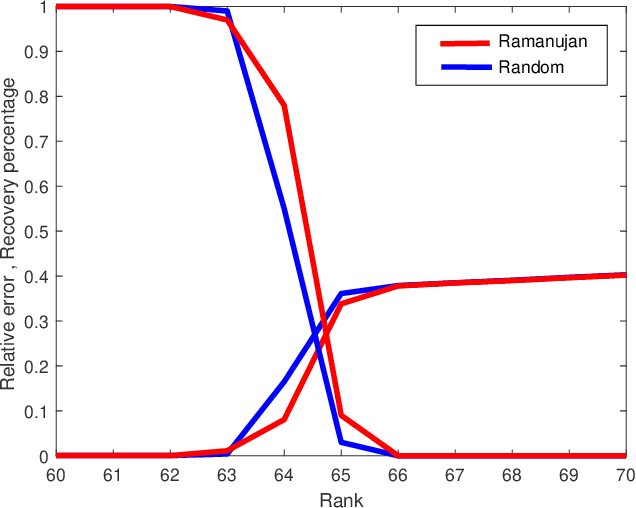
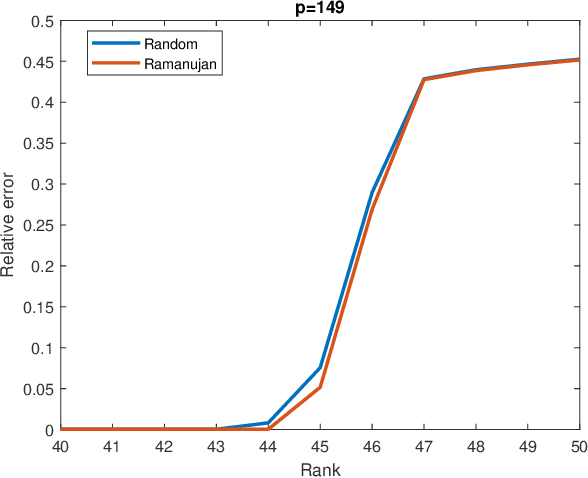
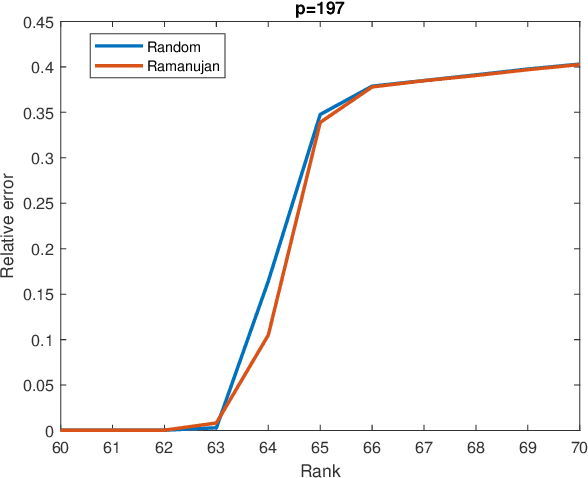
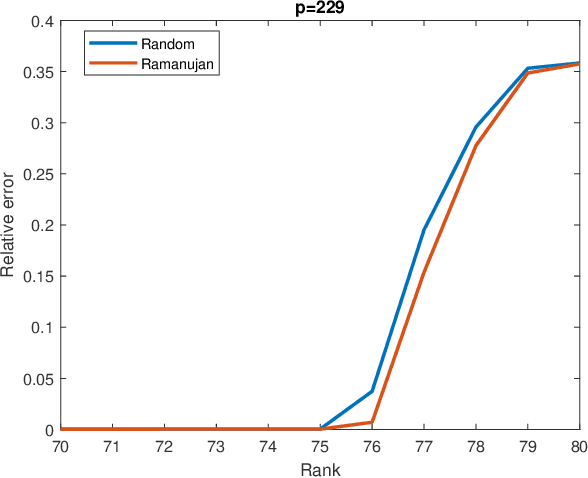
Matrix completion is a part of compressed sensing, and refers to determining an unknown low-rank matrix from a relatively small number of samples of the elements of the matrix. The problem has applications in recommendation engines, sensor localization, quantum tomography etc. In a companion paper (Part-1), the first and second author showed that it is possible to guarantee exact completion of an unknown low rank matrix, if the sample set corresponds to the edge set of a Ramanujan bigraph. In this paper, we present for the first time an infinite family of unbalanced Ramanujan bigraphs with explicitly constructed biadjacency matrices. In addition, we also show how to construct the adjacency matrices for the currently available families of Ramanujan graphs. In an attempt to determine how close the sufficient condition presented in Part-1 is to being necessary, we carried out numerical simulations of nuclear norm minimization on randomly generated low-rank matrices. The results revealed several noteworthy points, the most interesting of which is the existence of a phase transition. For square matrices, the maximum rank $\bar{r}$ for which nuclear norm minimization correctly completes all low-rank matrices is approximately $\bar{r} \approx d/3$, where $d$ is the degree of the Ramanujan graph. This upper limit appears to be independent of the specific family of Ramanujan graphs. The percentage of low-rank matrices that are recovered changes from 100% to 0% if the rank is increased by just two beyond $\bar{r}$. Again, this phenomenon appears to be independent of the specific family of Ramanujan graphs.

Deterministic Completion of Rectangular Matrices Using Asymmetric Ramanujan Graphs

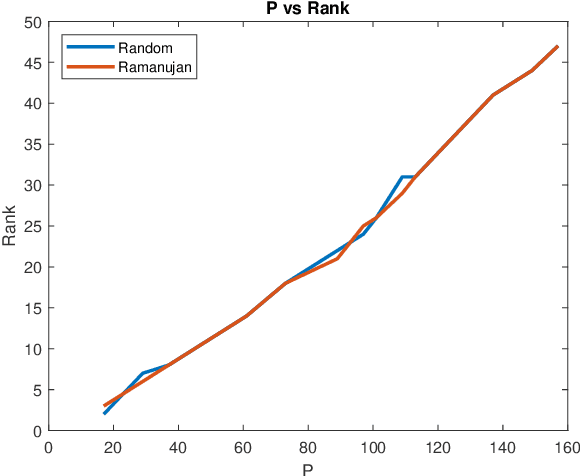
In this paper we study the matrix completion problem: Suppose $X \in \mathbb{R}^{n_r \times n_c}$ is unknown except for an upper bound $r$ on its rank. By measuring a small number $m \ll n_r n_c$ of elements of $X$, is it possible to recover $X$ exactly, or at least, to construct a reasonable approximation of $X$? There are two approaches to choosing the sample set, namely probabilistic and deterministic. At present there are very few deterministic methods, and they apply only to square matrices. The focus in the present paper is on deterministic methods that work for rectangular as well as square matrices. The elements to be sampled are chosen as the edge set of an asymmetric Ramanujan graph. For such a measurement matrix, we derive bounds on the error between a scaled version of the sampled matrix and unknown matrix, and show that, under suitable conditions, the unknown matrix can be recovered exactly. Even for the case of square matrices, these bounds are an improvement on known results. Of course they are entirely new for rectangular matrices. This raises the question of how such asymmetric Ramanujan graphs might be constructed. While some techniques exist for constructing Ramanujan bipartite graphs with equal numbers of vertices on both sides, until now no methods exist for constructing Ramanujan bipartite graphs with unequal numbers of vertices on the two sides. We provide a method for the construction of an infinite family of asymmetric biregular Ramanujan graphs with $q^2$ left vertices and $lq$ right vertices, where $q$ is any prime number and $l$ is any integer between $2$ and $q$. The left degree is $l$ and the right degree is $q$. So far as the authors are aware, this is the first explicit construction of an infinite family of asymmetric Ramanujan graphs.