Deterministic Completion of Rectangular Matrices Using Ramanujan Bigraphs -- II: Explicit Constructions and Phase Transitions
Paper and Code
Oct 08, 2019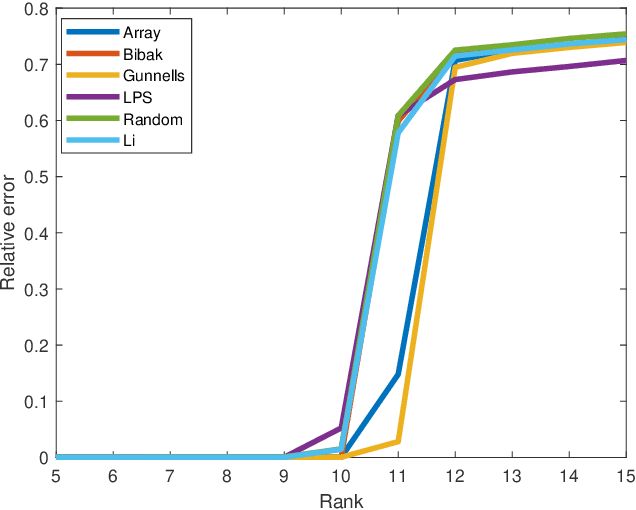
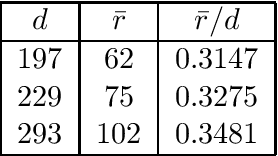
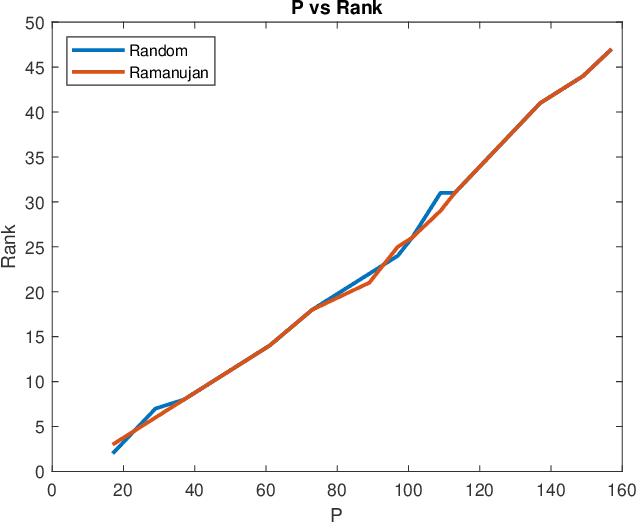
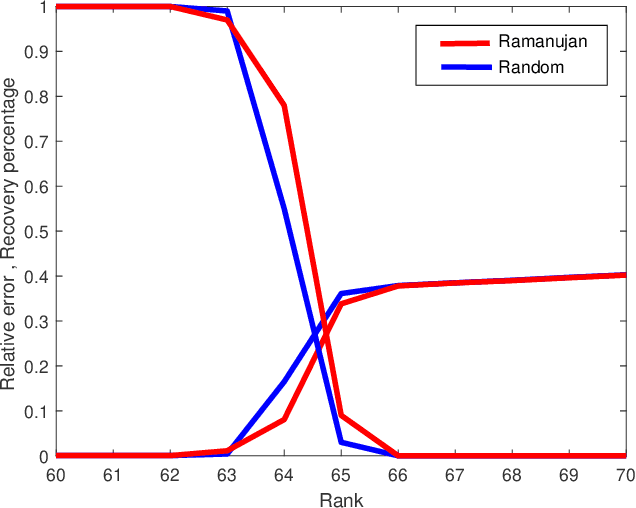
Matrix completion is a part of compressed sensing, and refers to determining an unknown low-rank matrix from a relatively small number of samples of the elements of the matrix. The problem has applications in recommendation engines, sensor localization, quantum tomography etc. In a companion paper (Part-1), the first and second author showed that it is possible to guarantee exact completion of an unknown low rank matrix, if the sample set corresponds to the edge set of a Ramanujan bigraph. In this paper, we present for the first time an infinite family of unbalanced Ramanujan bigraphs with explicitly constructed biadjacency matrices. In addition, we also show how to construct the adjacency matrices for the currently available families of Ramanujan graphs. In an attempt to determine how close the sufficient condition presented in Part-1 is to being necessary, we carried out numerical simulations of nuclear norm minimization on randomly generated low-rank matrices. The results revealed several noteworthy points, the most interesting of which is the existence of a phase transition. For square matrices, the maximum rank $\bar{r}$ for which nuclear norm minimization correctly completes all low-rank matrices is approximately $\bar{r} \approx d/3$, where $d$ is the degree of the Ramanujan graph. This upper limit appears to be independent of the specific family of Ramanujan graphs. The percentage of low-rank matrices that are recovered changes from 100% to 0% if the rank is increased by just two beyond $\bar{r}$. Again, this phenomenon appears to be independent of the specific family of Ramanujan graphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge