3-D Material Style Transfer for Reconstructing Unknown Appearance in Complex Natural Materials

We propose a 3-D material style transfer framework for reconstructing invisible (or faded) appearance properties in complex natural materials. Our algorithm addresses the technical challenge of transferring appearance properties from one object to another of the same material when both objects have intricate, noncorresponding color patterns. Eggshells, exoskeletons, and minerals, for example, have patterns composed of highly randomized layers of organic and inorganic compounds. These materials pose a challenge as the distribution of compounds that determine surface color changes from object to object and within local pattern regions. Our solution adapts appearance observations from a material property distribution in an exemplar to the material property distribution of a target object to reconstruct its unknown appearance. We use measured reflectance in 3-D bispectral textures to record changing material property distributions. Our novel implementation of spherical harmonics uses principles from chemistry and biology to learn relationships between color (hue and saturation) and material composition and concentration in an exemplar. The encoded relationships are transformed to the property distribution of a target for color recovery and material assignment. Quantitative and qualitative evaluation methods show that we replicate color patterns more accurately than methods that only rely on shape correspondences and coarse-level perceptual differences. We demonstrate applications of our work for reconstructing color in extinct fossils, restoring faded artifacts and generating synthetic textures.

Non-Photorealistic Rendering of Layered Materials: A Multispectral Approach

We present multispectral rendering techniques for visualizing layered materials found in biological specimens. We are the first to use acquired data from the near-infrared and ultraviolet spectra for non-photorealistic rendering (NPR). Several plant and animal species are more comprehensively understood by multispectral analysis. However, traditional NPR techniques ignore unique information outside the visible spectrum. We introduce algorithms and principles for processing wavelength dependent surface normals and reflectance. Our registration and feature detection methods are used to formulate stylization effects not considered by current NPR methods including: Spectral Band Shading which isolates and emphasizes shape features at specific wavelengths at multiple scales. Experts in our user study demonstrate the effectiveness of our system for applications in the biological sciences.

Tight Performance Bounds for Compressed Sensing With Conventional and Group Sparsity

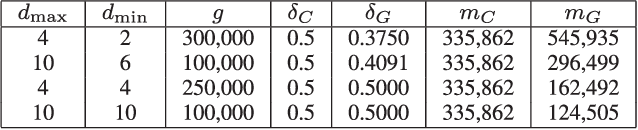
In this paper, we study the problem of recovering a group sparse vector from a small number of linear measurements. In the past the common approach has been to use various "group sparsity-inducing" norms such as the Group LASSO norm for this purpose. By using the theory of convex relaxations, we show that it is also possible to use $\ell_1$-norm minimization for group sparse recovery. We introduce a new concept called group robust null space property (GRNSP), and show that, under suitable conditions, a group version of the restricted isometry property (GRIP) implies the GRNSP, and thus leads to group sparse recovery. When all groups are of equal size, our bounds are less conservative than known bounds. Moreover, our results apply even to situations where where the groups have different sizes. When specialized to conventional sparsity, our bounds reduce to one of the well-known "best possible" conditions for sparse recovery. This relationship between GRNSP and GRIP is new even for conventional sparsity, and substantially streamlines the proofs of some known results. Using this relationship, we derive bounds on the $\ell_p$-norm of the residual error vector for all $p \in [1,2]$, and not just when $p = 2$. When the measurement matrix consists of random samples of a sub-Gaussian random variable, we present bounds on the number of measurements, which are less conservative than currently known bounds.