Convergence of Momentum-Based Heavy Ball Method with Batch Updating and/or Approximate Gradients

In this paper, we study the well-known "Heavy Ball" method for convex and nonconvex optimization introduced by Polyak in 1964, and establish its convergence under a variety of situations. Traditionally, most algorthms use "full-coordinate update," that is, at each step, very component of the argument is updated. However, when the dimension of the argument is very high, it is more efficient to update some but not all components of the argument at each iteration. We refer to this as "batch updating" in this paper. When gradient-based algorithms are used together with batch updating, in principle it is sufficient to compute only those components of the gradient for which the argument is to be updated. However, if a method such as back propagation is used to compute these components, computing only some components of gradient does not offer much savings over computing the entire gradient. Therefore, to achieve a noticeable reduction in CPU usage at each step, one can use first-order differences to approximate the gradient. The resulting estimates are biased, and also have unbounded variance. Thus some delicate analysis is required to ensure that the HB algorithm converge when batch updating is used instead of full-coordinate updating, and/or approximate gradients are used instead of true gradients. In this paper, we not only establish the almost sure convergence of the iterations to the stationary point(s) of the objective function, but also derive upper bounds on the rate of convergence. To the best of our knowledge, there is no other paper that combines all of these features.

Evince the artifacts of Spoof Speech by blending Vocal Tract and Voice Source Features

With the rapid advancement in synthetic speech generation technologies, great interest in differentiating spoof speech from the natural speech is emerging in the research community. The identification of these synthetic signals is a difficult task not only for the cutting-edge classification models but also for humans themselves. To prevent potential adverse effects, it becomes crucial to detect spoof signals. From a forensics perspective, it is also important to predict the algorithm which generated them to identify the forger. This needs an understanding of the underlying attributes of spoof signals which serve as a signature for the synthesizer. This study emphasizes the segments of speech signals critical in identifying their authenticity by utilizing the Vocal Tract System(\textit{VTS}) and Voice Source(\textit{VS}) features. In this paper, we propose a system that detects spoof signals as well as identifies the corresponding speech-generating algorithm. We achieve 99.58\% in algorithm classification accuracy. From experiments, we found that a VS feature-based system gives more attention to the transition of phonemes, while, a VTS feature-based system gives more attention to stationary segments of speech signals. We perform model fusion techniques on the VS-based and VTS-based systems to exploit the complementary information to develop a robust classifier. Upon analyzing the confusion plots we found that WaveRNN is poorly classified depicting more naturalness. On the other hand, we identified that synthesizer like Waveform Concatenation, and Neural Source Filter is classified with the highest accuracy. Practical implications of this work can aid researchers from both forensics (leverage artifacts) and the speech communities (mitigate artifacts).

Convergence of Batch Stochastic Gradient Descent Methods with Approximate Gradients and/or Noisy Measurements: Theory and Computational Results

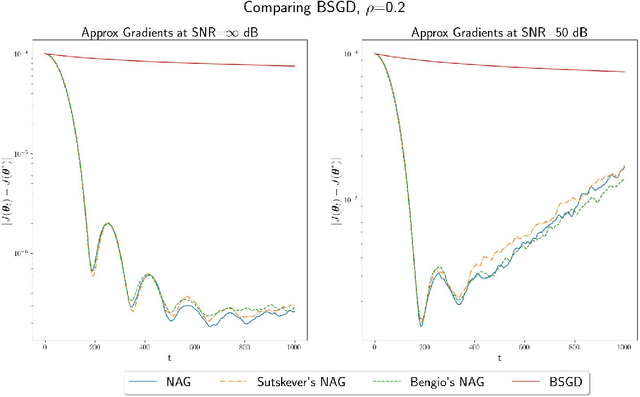
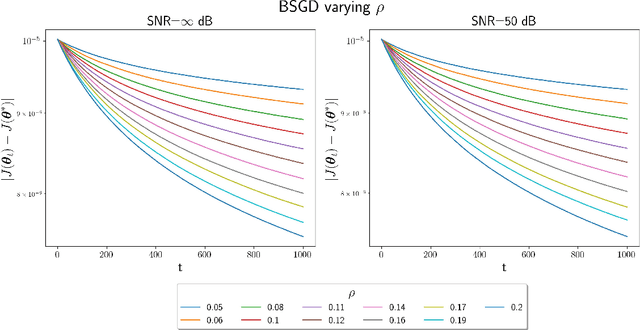
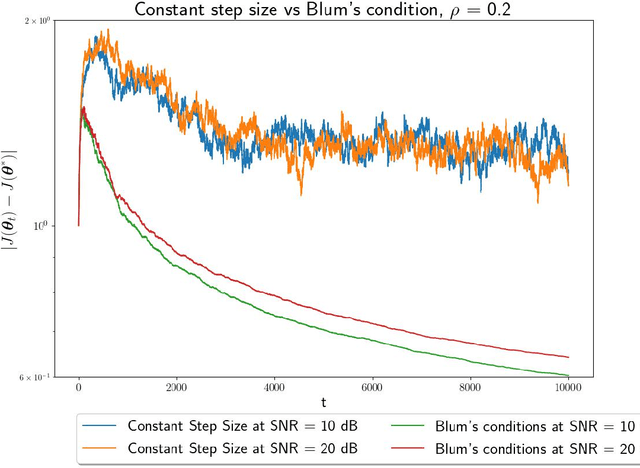
In this paper, we study convex optimization using a very general formulation called BSGD (Block Stochastic Gradient Descent). At each iteration, some but not necessary all components of the argument are updated. The direction of the update can be one of two possibilities: (i) A noise-corrupted measurement of the true gradient, or (ii) an approximate gradient computed using a first-order approximation, using function values that might themselves be corrupted by noise. This formulation embraces most of the currently used stochastic gradient methods. We establish conditions for BSGD to converge to the global minimum, based on stochastic approximation theory. Then we verify the predicted convergence through numerical experiments. Out results show that when approximate gradients are used, BSGD converges while momentum-based methods can diverge. However, not just our BSGD, but also standard (full-update) gradient descent, and various momentum-based methods, all converge, even with noisy gradients.