Convergence Rates for Stochastic Approximation: Biased Noise with Unbounded Variance, and Applications

The Stochastic Approximation (SA) algorithm introduced by Robbins and Monro in 1951 has been a standard method for solving equations of the form $\mathbf{f}({\boldsymbol {\theta}}) = \mathbf{0}$, when only noisy measurements of $\mathbf{f}(\cdot)$ are available. If $\mathbf{f}({\boldsymbol {\theta}}) = \nabla J({\boldsymbol {\theta}})$ for some function $J(\cdot)$, then SA can also be used to find a stationary point of $J(\cdot)$. In much of the literature, it is assumed that the error term ${\boldsymbol {xi}}_{t+1}$ has zero conditional mean, and that its conditional variance is bounded as a function of $t$ (though not necessarily with respect to ${\boldsymbol {\theta}}_t$). Also, for the most part, the emphasis has been on ``synchronous'' SA, whereby, at each time $t$, \textit{every} component of ${\boldsymbol {\theta}}_t$ is updated. Over the years, SA has been applied to a variety of areas, out of which two are the focus in this paper: Convex and nonconvex optimization, and Reinforcement Learning (RL). As it turns out, in these applications, the above-mentioned assumptions do not always hold. In zero-order methods, the error neither has zero mean nor bounded conditional variance. In the present paper, we extend SA theory to encompass errors with nonzero conditional mean and/or unbounded conditional variance, and also asynchronous SA. In addition, we derive estimates for the rate of convergence of the algorithm. Then we apply the new results to problems in nonconvex optimization, and to Markovian SA, a recently emerging area in RL. We prove that SA converges in these situations, and compute the ``optimal step size sequences'' to maximize the estimated rate of convergence.

Convergence of Batch Stochastic Gradient Descent Methods with Approximate Gradients and/or Noisy Measurements: Theory and Computational Results

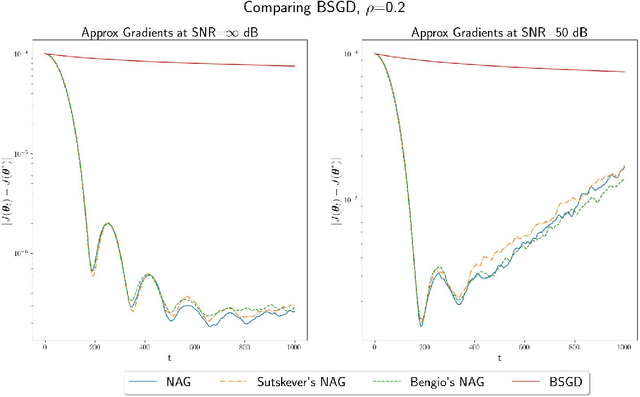
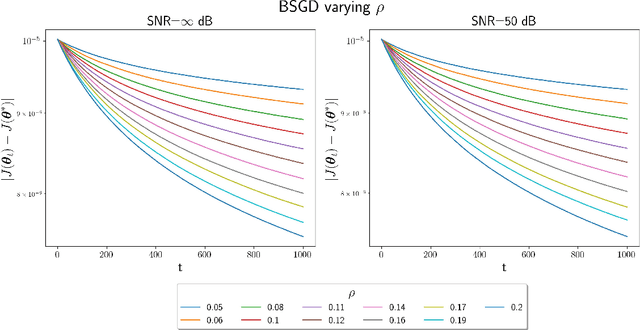
In this paper, we study convex optimization using a very general formulation called BSGD (Block Stochastic Gradient Descent). At each iteration, some but not necessary all components of the argument are updated. The direction of the update can be one of two possibilities: (i) A noise-corrupted measurement of the true gradient, or (ii) an approximate gradient computed using a first-order approximation, using function values that might themselves be corrupted by noise. This formulation embraces most of the currently used stochastic gradient methods. We establish conditions for BSGD to converge to the global minimum, based on stochastic approximation theory. Then we verify the predicted convergence through numerical experiments. Out results show that when approximate gradients are used, BSGD converges while momentum-based methods can diverge. However, not just our BSGD, but also standard (full-update) gradient descent, and various momentum-based methods, all converge, even with noisy gradients.

Convergence of Stochastic Approximation via Martingale and Converse Lyapunov Methods

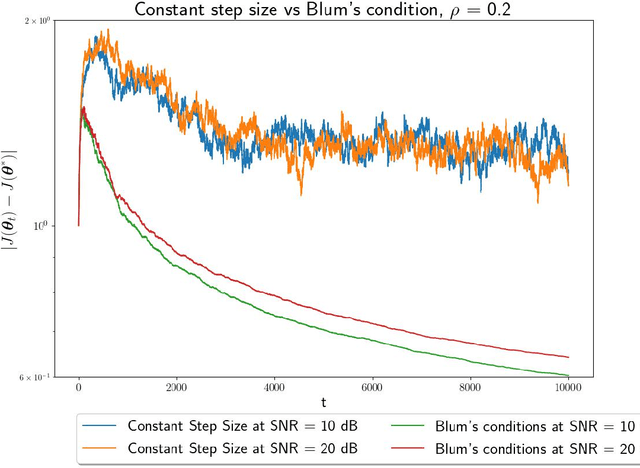
This paper is dedicated to Prof. Eduardo Sontag on the occasion of his seventieth birthday. In this paper, we build upon the ideas first proposed in Gladyshev (1965) to develop a very general framework for proving the almost sure boundedness and the convergence of stochastic approximation algorithms. These ideas are based on martingale methods and are in some ways simpler than convergence proofs based on the ODE method, e.g., Borkar-Meyn (2000). First we study the original version of the SA algorithm introduced in Robbins-Monro (1951), where the objective is to determine a zero of a function, when only noisy measurements of the function are available. The proof makes use of the general framework developed here, together with a new theorem on converse Lyapunov stability, which might be of independent interest. Next we study an alternate version of SA, first introduced in Kiefer-Wolfowitz (1952). The objective here is to find a stationary point of a scalar-valued function, using first-order differences to approximate its gradient. This problem is analyzed in Blum (1954), but with a very opaque proof. We reproduce Blum's conclusions using the proposed framework.

Convergence of Batch Asynchronous Stochastic Approximation With Applications to Reinforcement Learning

The stochastic approximation (SA) algorithm is a widely used probabilistic method for finding a solution to an equation of the form $\mathbf{f}(\boldsymbol{\theta}) = \mathbf{0}$ where $\mathbf{f} : \mathbb{R}^d \rightarrow \mathbb{R}^d$, when only noisy measurements of $\mathbf{f}(\cdot)$ are available. In the literature to date, one can make a distinction between "synchronous" updating, whereby the entire vector of the current guess $\boldsymbol{\theta}_t$ is updated at each time, and "asynchronous" updating, whereby ony one component of $\boldsymbol{\theta}_t$ is updated. In convex and nonconvex optimization, there is also the notion of "batch" updating, whereby some but not all components of $\boldsymbol{\theta}_t$ are updated at each time $t$. In addition, there is also a distinction between using a "local" clock versus a "global" clock. In the literature to date, convergence proofs when a local clock is used make the assumption that the measurement noise is an i.i.d\ sequence, an assumption that does not hold in Reinforcement Learning (RL). In this note, we provide a general theory of convergence for batch asymchronous stochastic approximation (BASA), that works whether the updates use a local clock or a global clock, for the case where the measurement noises form a martingale difference sequence. This is the most general result to date and encompasses all others.

Error Bounds for Compressed Sensing Algorithms With Group Sparsity: A Unified Approach

In compressed sensing, in order to recover a sparse or nearly sparse vector from possibly noisy measurements, the most popular approach is $\ell_1$-norm minimization. Upper bounds for the $\ell_2$- norm of the error between the true and estimated vectors are given in [1] and reviewed in [2], while bounds for the $\ell_1$-norm are given in [3]. When the unknown vector is not conventionally sparse but is "group sparse" instead, a variety of alternatives to the $\ell_1$-norm have been proposed in the literature, including the group LASSO, sparse group LASSO, and group LASSO with tree structured overlapping groups. However, no error bounds are available for any of these modified objective functions. In the present paper, a unified approach is presented for deriving upper bounds on the error between the true vector and its approximation, based on the notion of decomposable and $\gamma$-decomposable norms. The bounds presented cover all of the norms mentioned above, and also provide a guideline for choosing norms in future to accommodate alternate forms of sparsity.