Convergence Rates for Stochastic Approximation: Biased Noise with Unbounded Variance, and Applications

The Stochastic Approximation (SA) algorithm introduced by Robbins and Monro in 1951 has been a standard method for solving equations of the form $\mathbf{f}({\boldsymbol {\theta}}) = \mathbf{0}$, when only noisy measurements of $\mathbf{f}(\cdot)$ are available. If $\mathbf{f}({\boldsymbol {\theta}}) = \nabla J({\boldsymbol {\theta}})$ for some function $J(\cdot)$, then SA can also be used to find a stationary point of $J(\cdot)$. In much of the literature, it is assumed that the error term ${\boldsymbol {xi}}_{t+1}$ has zero conditional mean, and that its conditional variance is bounded as a function of $t$ (though not necessarily with respect to ${\boldsymbol {\theta}}_t$). Also, for the most part, the emphasis has been on ``synchronous'' SA, whereby, at each time $t$, \textit{every} component of ${\boldsymbol {\theta}}_t$ is updated. Over the years, SA has been applied to a variety of areas, out of which two are the focus in this paper: Convex and nonconvex optimization, and Reinforcement Learning (RL). As it turns out, in these applications, the above-mentioned assumptions do not always hold. In zero-order methods, the error neither has zero mean nor bounded conditional variance. In the present paper, we extend SA theory to encompass errors with nonzero conditional mean and/or unbounded conditional variance, and also asynchronous SA. In addition, we derive estimates for the rate of convergence of the algorithm. Then we apply the new results to problems in nonconvex optimization, and to Markovian SA, a recently emerging area in RL. We prove that SA converges in these situations, and compute the ``optimal step size sequences'' to maximize the estimated rate of convergence.

Convergence of Batch Stochastic Gradient Descent Methods with Approximate Gradients and/or Noisy Measurements: Theory and Computational Results

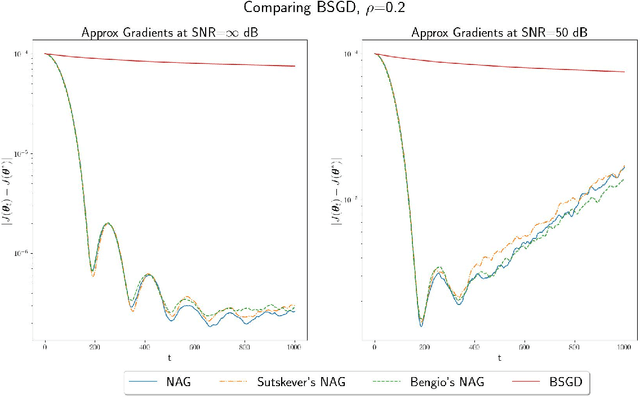
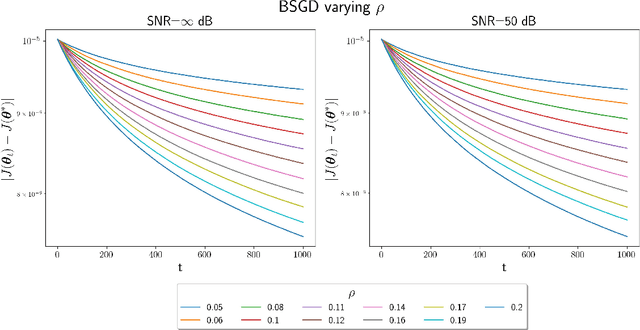
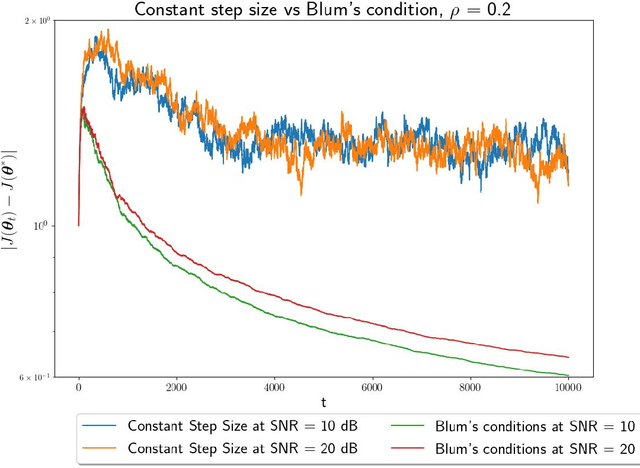
In this paper, we study convex optimization using a very general formulation called BSGD (Block Stochastic Gradient Descent). At each iteration, some but not necessary all components of the argument are updated. The direction of the update can be one of two possibilities: (i) A noise-corrupted measurement of the true gradient, or (ii) an approximate gradient computed using a first-order approximation, using function values that might themselves be corrupted by noise. This formulation embraces most of the currently used stochastic gradient methods. We establish conditions for BSGD to converge to the global minimum, based on stochastic approximation theory. Then we verify the predicted convergence through numerical experiments. Out results show that when approximate gradients are used, BSGD converges while momentum-based methods can diverge. However, not just our BSGD, but also standard (full-update) gradient descent, and various momentum-based methods, all converge, even with noisy gradients.

Convergence of Batch Asynchronous Stochastic Approximation With Applications to Reinforcement Learning

The stochastic approximation (SA) algorithm is a widely used probabilistic method for finding a solution to an equation of the form $\mathbf{f}(\boldsymbol{\theta}) = \mathbf{0}$ where $\mathbf{f} : \mathbb{R}^d \rightarrow \mathbb{R}^d$, when only noisy measurements of $\mathbf{f}(\cdot)$ are available. In the literature to date, one can make a distinction between "synchronous" updating, whereby the entire vector of the current guess $\boldsymbol{\theta}_t$ is updated at each time, and "asynchronous" updating, whereby ony one component of $\boldsymbol{\theta}_t$ is updated. In convex and nonconvex optimization, there is also the notion of "batch" updating, whereby some but not all components of $\boldsymbol{\theta}_t$ are updated at each time $t$. In addition, there is also a distinction between using a "local" clock versus a "global" clock. In the literature to date, convergence proofs when a local clock is used make the assumption that the measurement noise is an i.i.d\ sequence, an assumption that does not hold in Reinforcement Learning (RL). In this note, we provide a general theory of convergence for batch asymchronous stochastic approximation (BASA), that works whether the updates use a local clock or a global clock, for the case where the measurement noises form a martingale difference sequence. This is the most general result to date and encompasses all others.