Convergence of Batch Stochastic Gradient Descent Methods with Approximate Gradients and/or Noisy Measurements: Theory and Computational Results

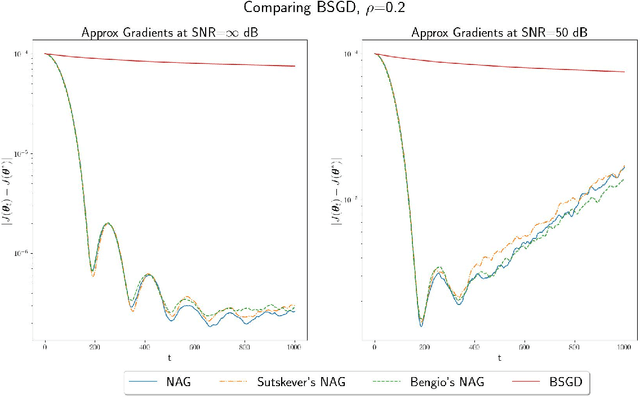
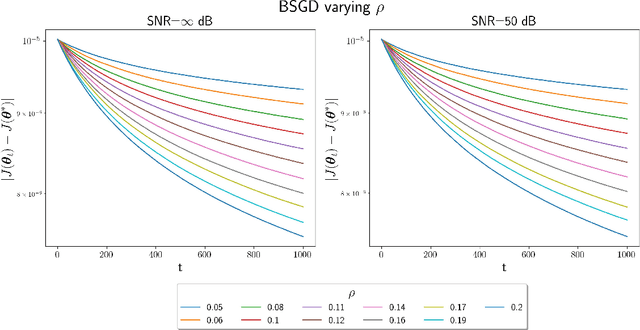
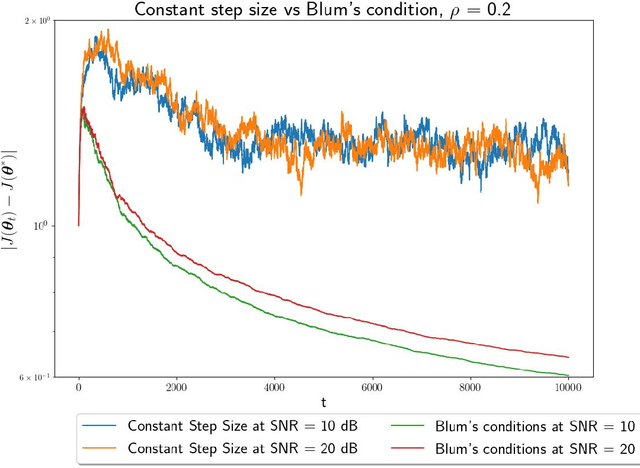
In this paper, we study convex optimization using a very general formulation called BSGD (Block Stochastic Gradient Descent). At each iteration, some but not necessary all components of the argument are updated. The direction of the update can be one of two possibilities: (i) A noise-corrupted measurement of the true gradient, or (ii) an approximate gradient computed using a first-order approximation, using function values that might themselves be corrupted by noise. This formulation embraces most of the currently used stochastic gradient methods. We establish conditions for BSGD to converge to the global minimum, based on stochastic approximation theory. Then we verify the predicted convergence through numerical experiments. Out results show that when approximate gradients are used, BSGD converges while momentum-based methods can diverge. However, not just our BSGD, but also standard (full-update) gradient descent, and various momentum-based methods, all converge, even with noisy gradients.