Compressed Sensing Using Binary Matrices of Nearly Optimal Dimensions

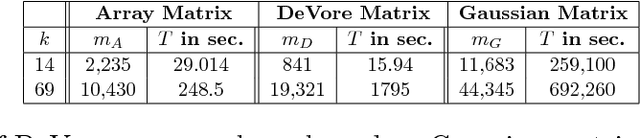
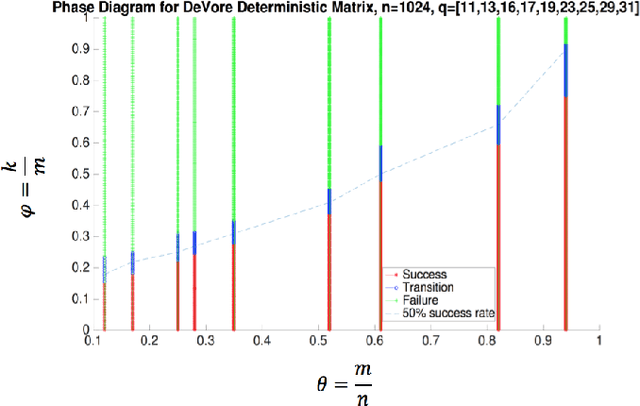
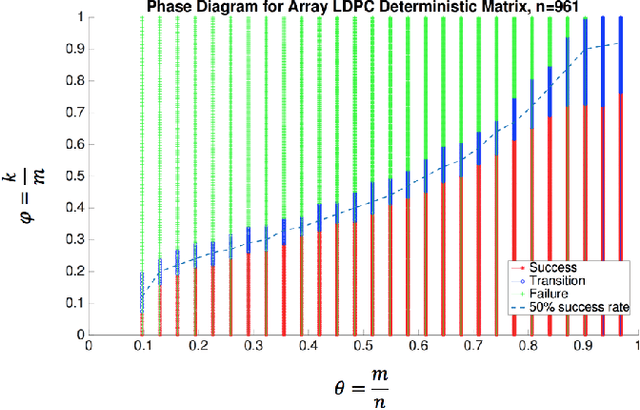
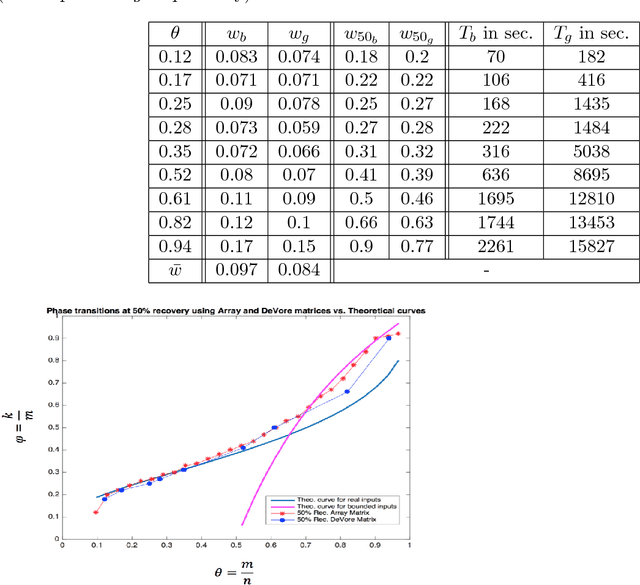
In this paper, we study the problem of compressed sensing using binary measurement matrices, and $\ell_1$-norm minimization (basis pursuit) as the recovery algorithm. We derive new upper and lower bounds on the number of measurements to achieve robust sparse recovery with binary matrices. We establish sufficient conditions for a column-regular binary matrix to satisfy the robust null space property (RNSP), and show that the sparsity bounds for robust sparse recovery obtained using the RNSP are better by a factor of $(3 \sqrt{3})/2 \approx 2.6$ compared to the restricted isometry property (RIP). Next we derive universal \textit{lower} bounds on the number of measurements that any binary matrix needs to have in order to satisfy the weaker sufficient condition based on the RNSP, and show that bipartite graphs of girth six are optimal. Then we display two classes of binary matrices, namely parity check matrices of array codes, and Euler squares, that have girth six and are nearly optimal in the sense of almost satisfying the lower bound. In principle randomly generated Gaussian measurement matrices are `order-optimal.' So we compare the phase transition behavior of the basis pursuit formulation using binary array code and Gaussian matrices, and show that (i) there is essentially no difference between the phase transition boundaries in the two cases, and (ii) the CPU time of basis pursuit with binary matrices is hundreds of times faster than with Gaussian matrices, and the storage requirements are less. Therefore it is suggested that binary matrices are a viable alternative to Gaussian matrices for compressed sensing using basis pursuit.