Safe Exploration for Identifying Linear Systems via Robust Optimization

Safely exploring an unknown dynamical system is critical to the deployment of reinforcement learning (RL) in physical systems where failures may have catastrophic consequences. In scenarios where one knows little about the dynamics, diverse transition data covering relevant regions of state-action space is needed to apply either model-based or model-free RL. Motivated by the cooling of Google's data centers, we study how one can safely identify the parameters of a system model with a desired accuracy and confidence level. In particular, we focus on learning an unknown linear system with Gaussian noise assuming only that, initially, a nominal safe action is known. Define safety as satisfying specific linear constraints on the state space (e.g., requirements on process variable) that must hold over the span of an entire trajectory, and given a Probably Approximately Correct (PAC) style bound on the estimation error of model parameters, we show how to compute safe regions of action space by gradually growing a ball around the nominal safe action. One can apply any exploration strategy where actions are chosen from such safe regions. Experiments on a stylized model of data center cooling dynamics show how computing proper safe regions can increase the sample efficiency of safe exploration.

On Local Regret

Online learning aims to perform nearly as well as the best hypothesis in hindsight. For some hypothesis classes, though, even finding the best hypothesis offline is challenging. In such offline cases, local search techniques are often employed and only local optimality guaranteed. For online decision-making with such hypothesis classes, we introduce local regret, a generalization of regret that aims to perform nearly as well as only nearby hypotheses. We then present a general algorithm to minimize local regret with arbitrary locality graphs. We also show how the graph structure can be exploited to drastically speed learning. These algorithms are then demonstrated on a diverse set of online problems: online disjunct learning, online Max-SAT, and online decision tree learning.

No-Regret Learning in Extensive-Form Games with Imperfect Recall

Counterfactual Regret Minimization (CFR) is an efficient no-regret learning algorithm for decision problems modeled as extensive games. CFR's regret bounds depend on the requirement of perfect recall: players always remember information that was revealed to them and the order in which it was revealed. In games without perfect recall, however, CFR's guarantees do not apply. In this paper, we present the first regret bound for CFR when applied to a general class of games with imperfect recall. In addition, we show that CFR applied to any abstraction belonging to our general class results in a regret bound not just for the abstract game, but for the full game as well. We verify our theory and show how imperfect recall can be used to trade a small increase in regret for a significant reduction in memory in three domains: die-roll poker, phantom tic-tac-toe, and Bluff.

Slow Learners are Fast

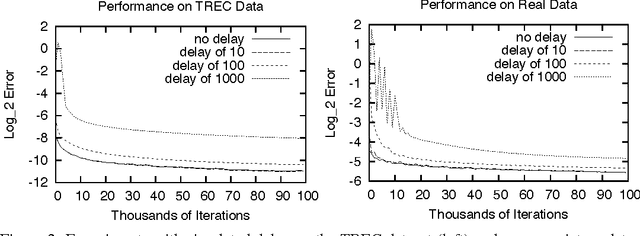
Online learning algorithms have impressive convergence properties when it comes to risk minimization and convex games on very large problems. However, they are inherently sequential in their design which prevents them from taking advantage of modern multi-core architectures. In this paper we prove that online learning with delayed updates converges well, thereby facilitating parallel online learning.