Quantification of total uncertainty in the physics-informed reconstruction of CVSim-6 physiology

When predicting physical phenomena through simulation, quantification of the total uncertainty due to multiple sources is as crucial as making sure the underlying numerical model is accurate. Possible sources include irreducible aleatoric uncertainty due to noise in the data, epistemic uncertainty induced by insufficient data or inadequate parameterization, and model-form uncertainty related to the use of misspecified model equations. Physics-based regularization interacts in nontrivial ways with aleatoric, epistemic and model-form uncertainty and their combination, and a better understanding of this interaction is needed to improve the predictive performance of physics-informed digital twins that operate under real conditions. With a specific focus on biological and physiological models, this study investigates the decomposition of total uncertainty in the estimation of states and parameters of a differential system simulated with MC X-TFC, a new physics-informed approach for uncertainty quantification based on random projections and Monte-Carlo sampling. MC X-TFC is applied to a six-compartment stiff ODE system, the CVSim-6 model, developed in the context of human physiology. The system is analyzed by progressively removing data while estimating an increasing number of parameters and by investigating total uncertainty under model-form misspecification of non-linear resistance in the pulmonary compartment. In particular, we focus on the interaction between the formulation of the discrepancy term and quantification of model-form uncertainty, and show how additional physics can help in the estimation process. The method demonstrates robustness and efficiency in estimating unknown states and parameters, even with limited, sparse, and noisy data. It also offers great flexibility in integrating data with physics for improved estimation, even in cases of model misspecification.

AI-Lorenz: A physics-data-driven framework for black-box and gray-box identification of chaotic systems with symbolic regression

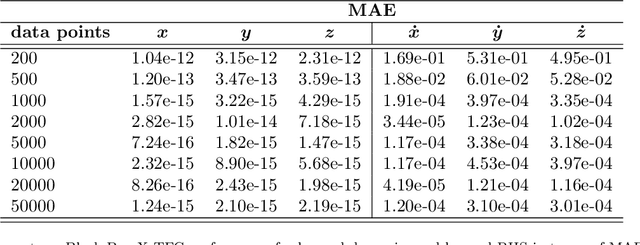
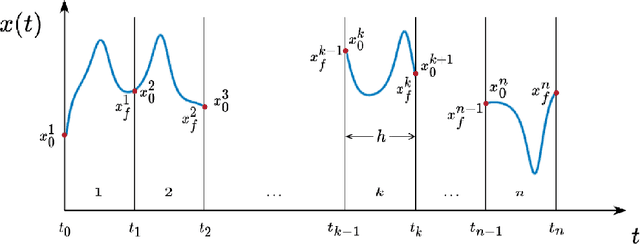
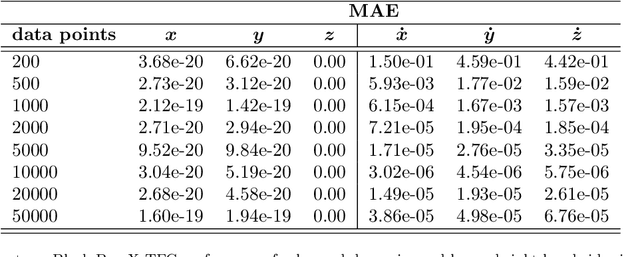
Discovering mathematical models that characterize the observed behavior of dynamical systems remains a major challenge, especially for systems in a chaotic regime. The challenge is even greater when the physics underlying such systems is not yet understood, and scientific inquiry must solely rely on empirical data. Driven by the need to fill this gap, we develop a framework that learns mathematical expressions modeling complex dynamical behaviors by identifying differential equations from noisy and sparse observable data. We train a small neural network to learn the dynamics of a system, its rate of change in time, and missing model terms, which are used as input for a symbolic regression algorithm to autonomously distill the explicit mathematical terms. This, in turn, enables us to predict the future evolution of the dynamical behavior. The performance of this framework is validated by recovering the right-hand sides and unknown terms of certain complex, chaotic systems such as the well-known Lorenz system, a six-dimensional hyperchaotic system, and the non-autonomous Sprott chaotic system, and comparing them with their known analytical expressions.

AI-Aristotle: A Physics-Informed framework for Systems Biology Gray-Box Identification

Discovering mathematical equations that govern physical and biological systems from observed data is a fundamental challenge in scientific research. We present a new physics-informed framework for parameter estimation and missing physics identification (gray-box) in the field of Systems Biology. The proposed framework -- named AI-Aristotle -- combines eXtreme Theory of Functional Connections (X-TFC) domain-decomposition and Physics-Informed Neural Networks (PINNs) with symbolic regression (SR) techniques for parameter discovery and gray-box identification. We test the accuracy, speed, flexibility and robustness of AI-Aristotle based on two benchmark problems in Systems Biology: a pharmacokinetics drug absorption model, and an ultradian endocrine model for glucose-insulin interactions. We compare the two machine learning methods (X-TFC and PINNs), and moreover, we employ two different symbolic regression techniques to cross-verify our results. While the current work focuses on the performance of AI-Aristotle based on synthetic data, it can equally handle noisy experimental data and can even be used for black-box identification in just a few minutes on a laptop. More broadly, our work provides insights into the accuracy, cost, scalability, and robustness of integrating neural networks with symbolic regressors, offering a comprehensive guide for researchers tackling gray-box identification challenges in complex dynamical systems in biomedicine and beyond.

Extreme Theory of Functional Connections: A Physics-Informed Neural Network Method for Solving Parametric Differential Equations

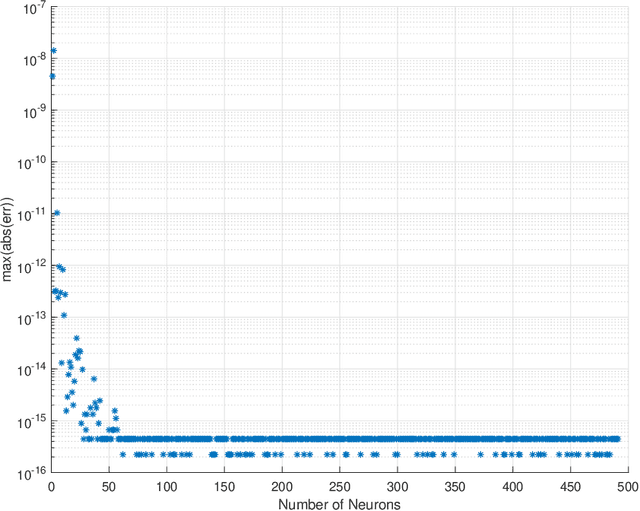
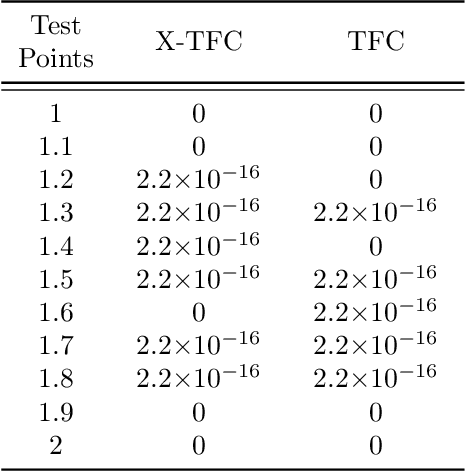
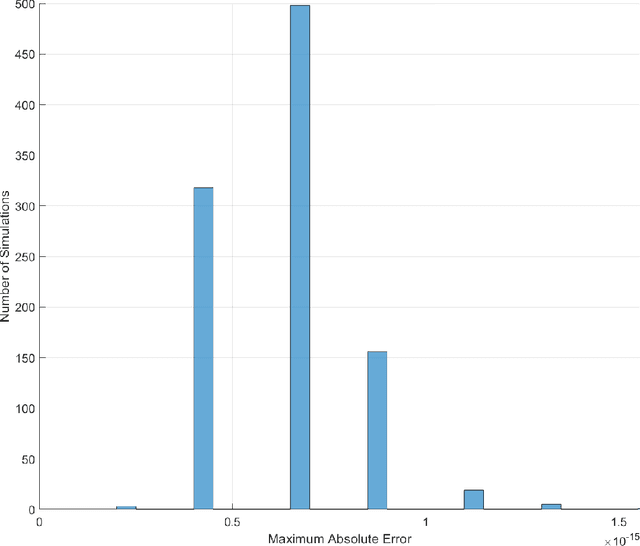
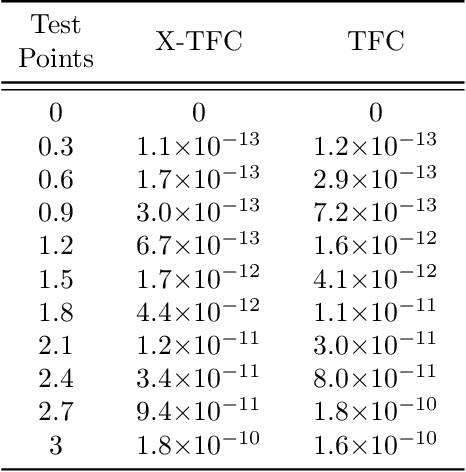
In this work we present a novel, accurate, and robust physics-informed method for solving problems involving parametric differential equations (DEs) called the Extreme Theory of Functional Connections, or X-TFC. The proposed method is a synergy of two recently developed frameworks for solving problems involving parametric DEs, 1) the Theory of Functional Connections, TFC, and the Physics-Informed Neural Networks, PINN. Although this paper focuses on the solution of exact problems involving parametric DEs (i.e. problems where the modeling error is negligible) with known parameters, X-TFC can also be used for data-driven solutions and data-driven discovery of parametric DEs. In the proposed method, the latent solution of the parametric DEs is approximated by a TFC constrained expression that uses a Neural Network (NN) as the free-function. This approximate solution form always analytically satisfies the constraints of the DE, while maintaining a NN with unconstrained parameters, like the Deep-TFC method. X-TFC differs from PINN and Deep-TFC; whereas PINN and Deep-TFC use a deep-NN, X-TFC uses a single-layer NN, or more precisely, an Extreme Learning Machine, ELM. This choice is based on the properties of the ELM algorithm. In order to numerically validate the method, it was tested over a range of problems including the approximation of solutions to linear and non-linear ordinary DEs (ODEs), systems of ODEs (SODEs), and partial DEs (PDEs). Furthermore, a few of these problems are of interest in physics and engineering such as the Classic Emden-Fowler equation, the Radiative Transfer (RT) equation, and the Heat-Transfer (HT) equation. The results show that X-TFC achieves high accuracy with low computational time and thus it is comparable with the other state-of-the-art methods.