Carl Leake
Flight Demonstration and Model Validation of a Prototype Variable-Altitude Venus Aerobot
Nov 11, 2024
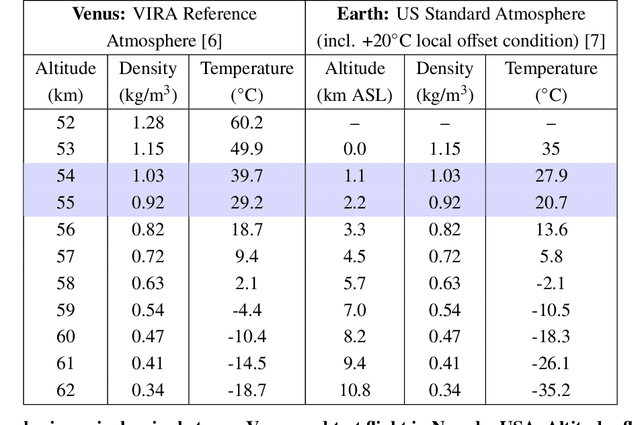

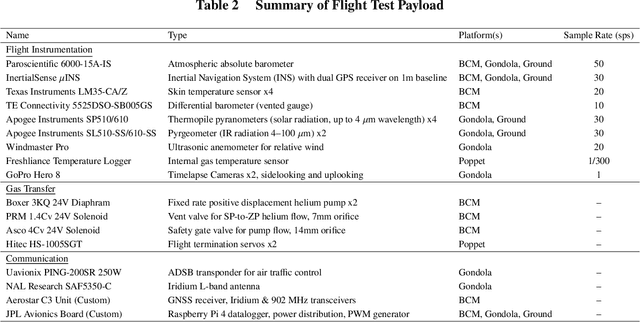
Abstract:This paper details a significant milestone towards maturing a buoyant aerial robotic platform, or aerobot, for flight in the Venus clouds. We describe two flights of our subscale altitude-controlled aerobot, fabricated from the materials necessary to survive Venus conditions. During these flights over the Nevada Black Rock desert, the prototype flew at the identical atmospheric densities as 54 to 55 km cloud layer altitudes on Venus. We further describe a first-principle aerobot dynamics model which we validate against the Nevada flight data and subsequently employ to predict the performance of future aerobots on Venus. The aerobot discussed in this paper is under JPL development for an in-situ mission flying multiple circumnavigations of Venus, sampling the chemical and physical properties of the planet's atmosphere and also remotely sensing surface properties.
Motivations and Preliminary Design for Mid-Air Deployment of a Science Rotorcraft on Mars
Oct 13, 2020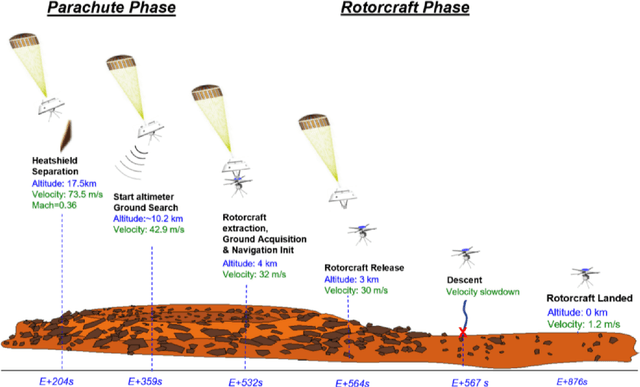
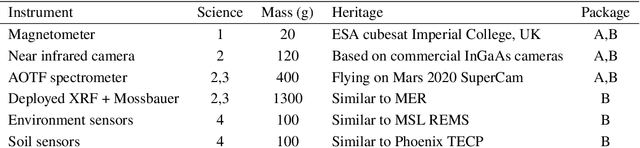
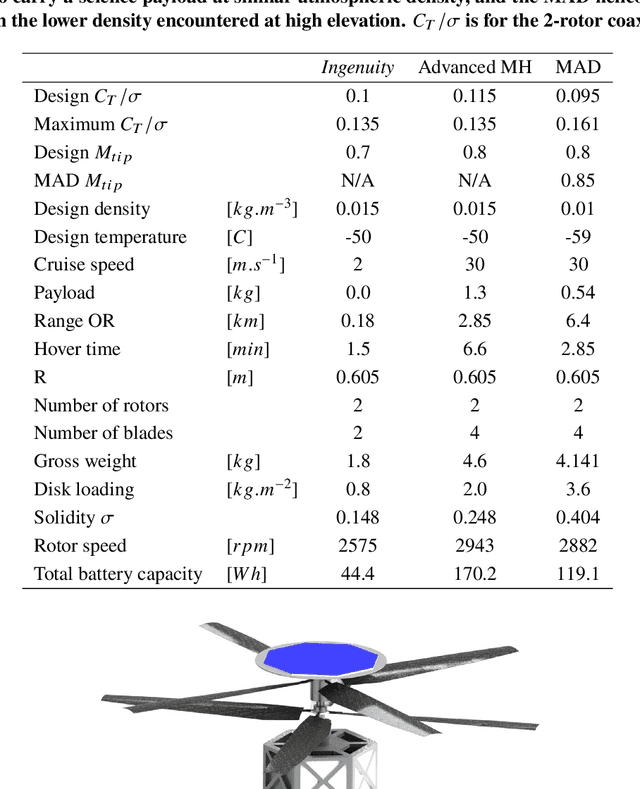
Abstract:Mid-Air Deployment (MAD) of a rotorcraft during Entry, Descent and Landing (EDL) on Mars eliminates the need to carry a propulsion or airbag landing system. This reduces the total mass inside the aeroshell by more than 100 kg and simplifies the aeroshell architecture. MAD's lighter and simpler design is likely to bring the risk and cost associated with the mission down. Moreover, the lighter entry mass enables landing in the Martian highlands, at elevations inaccessible to current EDL technologies. This paper proposes a novel MAD concept for a Mars helicopter. We suggest a minimum science payload package to perform relevant science in the highlands. A variant of the Ingenuity helicopter is proposed to provide increased deceleration during MAD, and enough lift to fly the science payload in the highlands. We show in simulation that the lighter aeroshell results in a lower terminal velocity (30 m/s) at the end of the parachute phase of the EDL, and at higher altitudes than other approaches. After discussing the aerodynamics, controls, guidance, and mechanical challenges associated with deploying at such speed, we propose a backshell architecture that addresses them to release the helicopter in the safest conditions. Finally, we implemented the helicopter model and aerodynamic descent perturbations in the JPL Dynamics and Real-Time Simulation (DARTS)framework. Preliminary performance evaluation indicates landing and helicopter operation scan be achieved up to 5 km MOLA (Mars Orbiter Laser Altimeter reference).
Extreme Theory of Functional Connections: A Physics-Informed Neural Network Method for Solving Parametric Differential Equations
May 15, 2020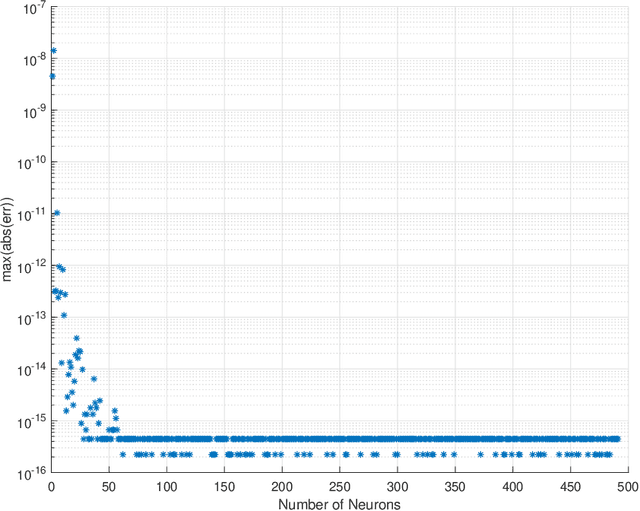
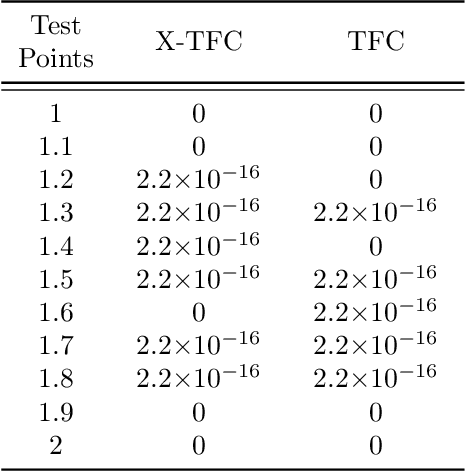
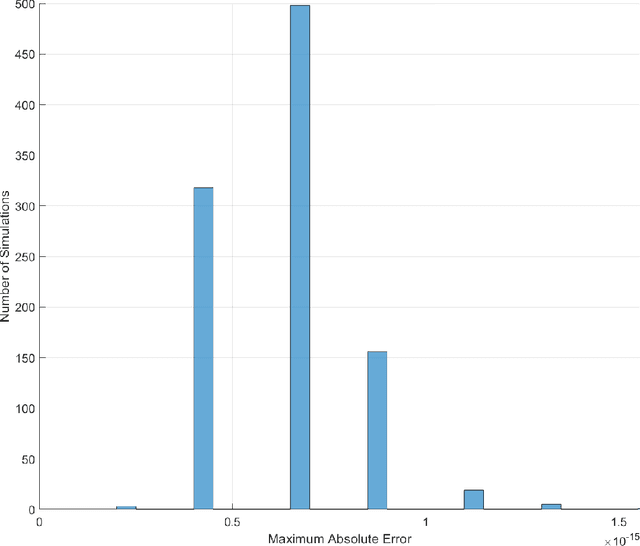
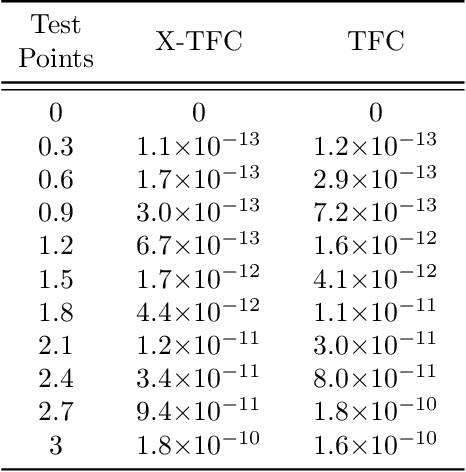
Abstract:In this work we present a novel, accurate, and robust physics-informed method for solving problems involving parametric differential equations (DEs) called the Extreme Theory of Functional Connections, or X-TFC. The proposed method is a synergy of two recently developed frameworks for solving problems involving parametric DEs, 1) the Theory of Functional Connections, TFC, and the Physics-Informed Neural Networks, PINN. Although this paper focuses on the solution of exact problems involving parametric DEs (i.e. problems where the modeling error is negligible) with known parameters, X-TFC can also be used for data-driven solutions and data-driven discovery of parametric DEs. In the proposed method, the latent solution of the parametric DEs is approximated by a TFC constrained expression that uses a Neural Network (NN) as the free-function. This approximate solution form always analytically satisfies the constraints of the DE, while maintaining a NN with unconstrained parameters, like the Deep-TFC method. X-TFC differs from PINN and Deep-TFC; whereas PINN and Deep-TFC use a deep-NN, X-TFC uses a single-layer NN, or more precisely, an Extreme Learning Machine, ELM. This choice is based on the properties of the ELM algorithm. In order to numerically validate the method, it was tested over a range of problems including the approximation of solutions to linear and non-linear ordinary DEs (ODEs), systems of ODEs (SODEs), and partial DEs (PDEs). Furthermore, a few of these problems are of interest in physics and engineering such as the Classic Emden-Fowler equation, the Radiative Transfer (RT) equation, and the Heat-Transfer (HT) equation. The results show that X-TFC achieves high accuracy with low computational time and thus it is comparable with the other state-of-the-art methods.
Non-dimensional Star-Identification
Mar 30, 2020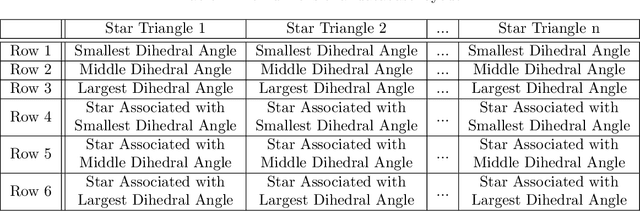
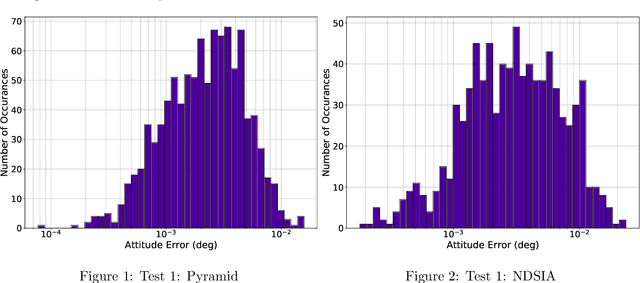
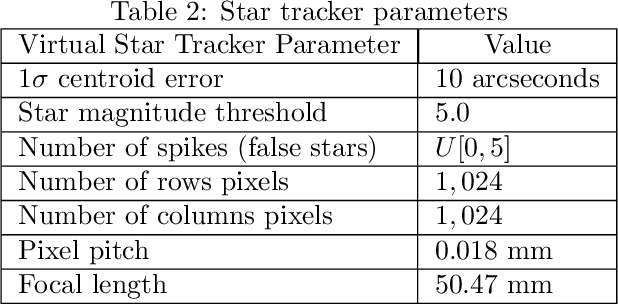
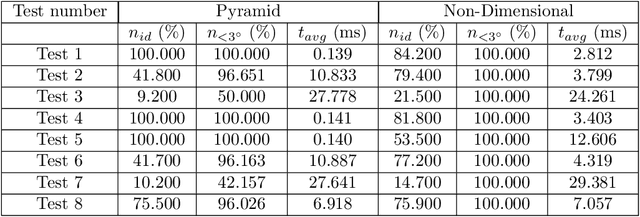
Abstract:This study introduces a new "Non-Dimensional" star identification algorithm to reliably identify the stars observed by a wide field-of-view star tracker when the focal length and optical axis offset values are known with poor accuracy. This algorithm is particularly suited to complement nominal lost-in-space algorithms when they fail the star identification due to focal length and/or optical axis offset deviations from their nominal operational ranges. These deviations may be caused, for example, by launch vibrations or thermal variations in orbit. The algorithm performance is compared in terms of accuracy, speed, and robustness to the Pyramid algorithm. These comparisons highlight the clear advantages that a combined approach of these methodologies provides.
Deep ToC: A New Method for Estimating the Solutions of PDEs
Dec 20, 2018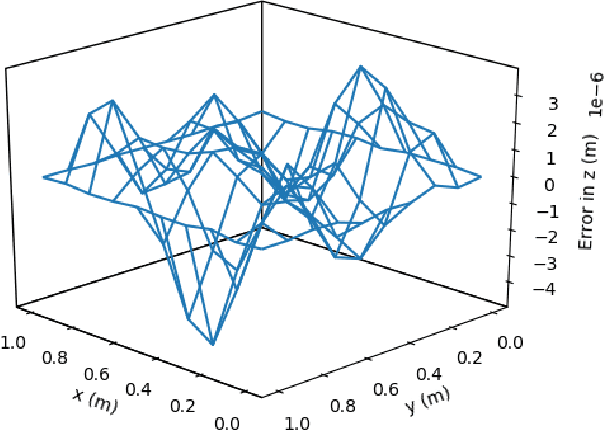
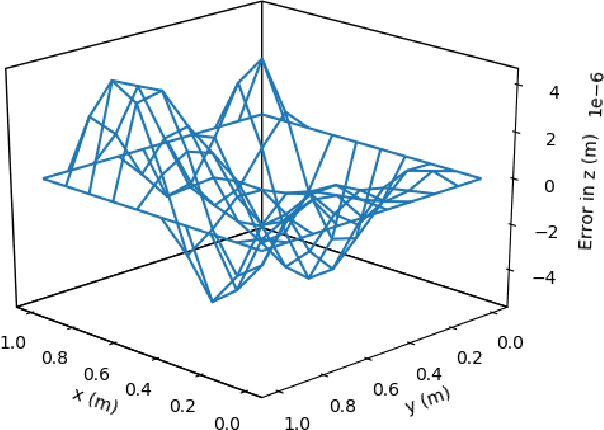
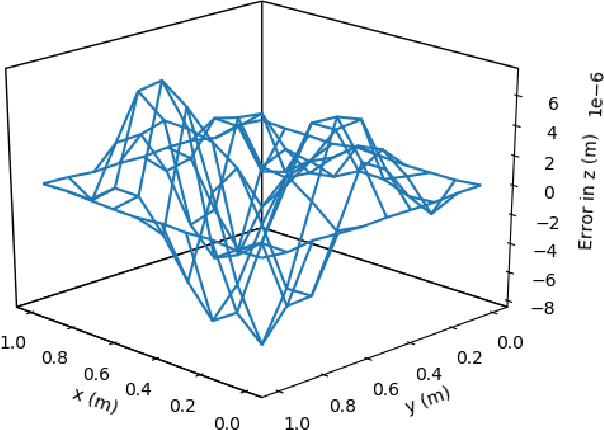
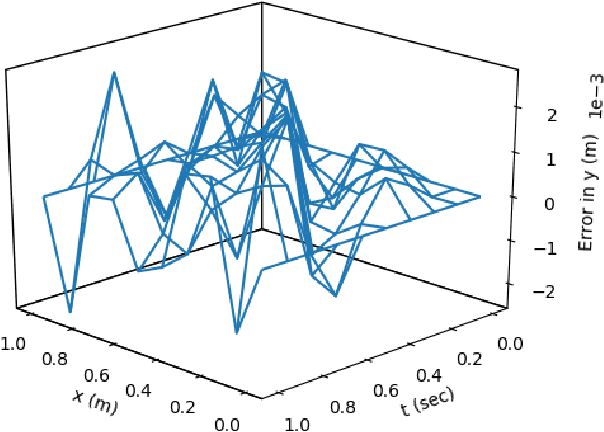
Abstract:This article presents a new methodology called deep ToC that estimates the solutions of partial differential equations (PDEs) by combining neural networks with the Theory of Connections (ToC). ToC is used to transform PDEs with boundary conditions into unconstrained optimization problems by embedding the boundary conditions into a "constrained expression" that contains a neural network. The loss function for the unconstrained optimization problem is taken to be the square of the residual of the PDE. Then, the neural network is trained in an unsupervised manner to solve the unconstrained optimization problem. This methodology has two major advantages over other popular methods used to estimate the solutions of PDEs. First, this methodology does not need to discretize the domain into a grid, which becomes prohibitive as the dimensionality of the PDE increases. Instead, this methodology randomly samples points from the domain during the training phase. Second, after training, this methodology represents a closed form, analytical, differentiable approximation of the solution throughout the entire training domain. In contrast, other popular methods require interpolation if the estimated solution is desired at points that do not lie on the discretized grid. The deep ToC method for estimating the solution of PDEs is demonstrated on four problems with a variety of boundary conditions.
Theory of Connections Applied to Support Vector Machines to Solve Differential Equations
Dec 13, 2018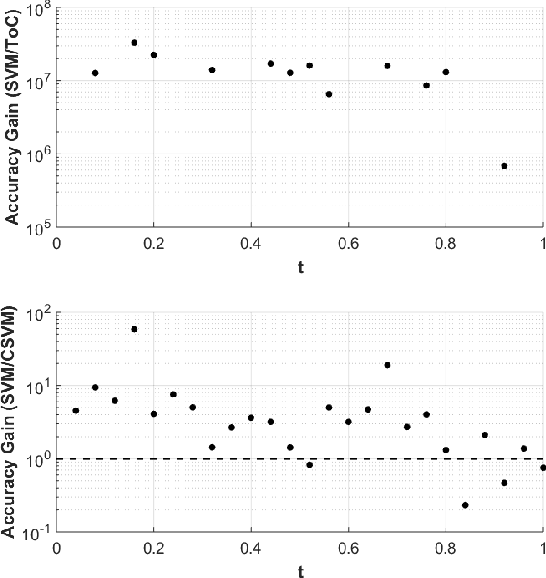
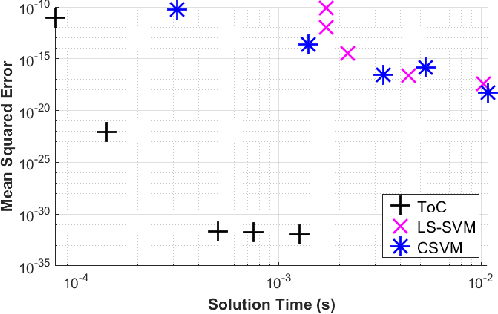
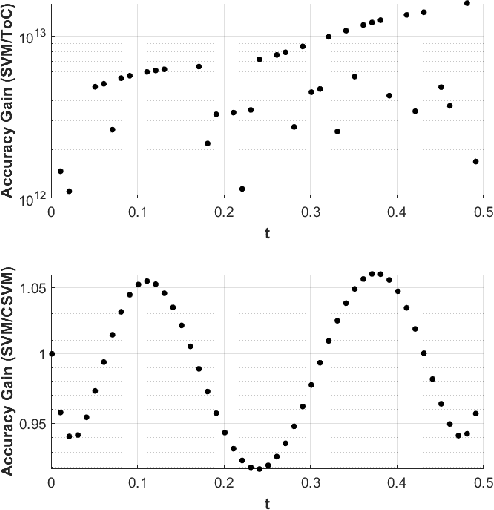
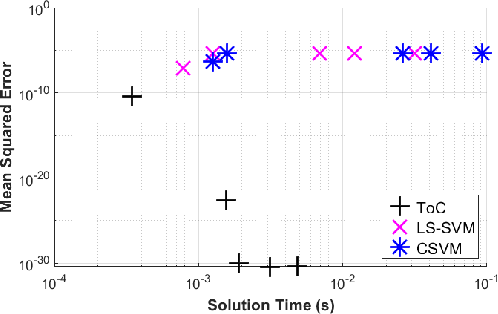
Abstract:Differential equations are used as numerical models to describe physical phenomena throughout the field of engineering and science, including heat and fluid flow, structural bending, and systems dynamics. Although there are many other techniques for finding approximate solutions to these equations, this paper looks to compare the application of the Theory of Connections (ToC) with one based on Support Vector Machines (SVM). The ToC method uses a constrained expression (an expression that always satisfies the differential equation constraints), which transforms the process of solving a differential equation into an unconstrained problem, and is ultimately solved via least-squares. In addition to individual analysis, the two methods are merged into a new methodology, called constrained SMVs (CSVM), by incorporating the SVM method into the ToC framework to solve unconstrained problems. Numerical tests are conducted on three sample problems: one first order linear ODEs, one first order non-linear ODE, and one second order linear ODE. Using the SVM method as a benchmark, a speed comparison is made for all the problems by timing the training period, and an accuracy comparison is made using the maximum error and mean-squared error on the training and test sets. In general, ToC is shown to be slightly faster (by an order of magnitude or less) and more accurate (by multiple orders of magnitude) over the SVM and CSVM approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge