Deep ToC: A New Method for Estimating the Solutions of PDEs

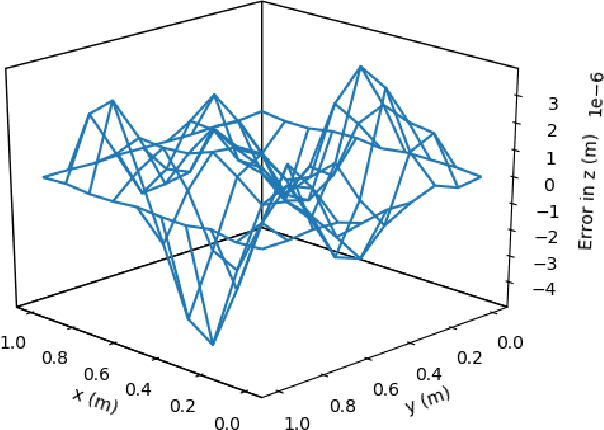
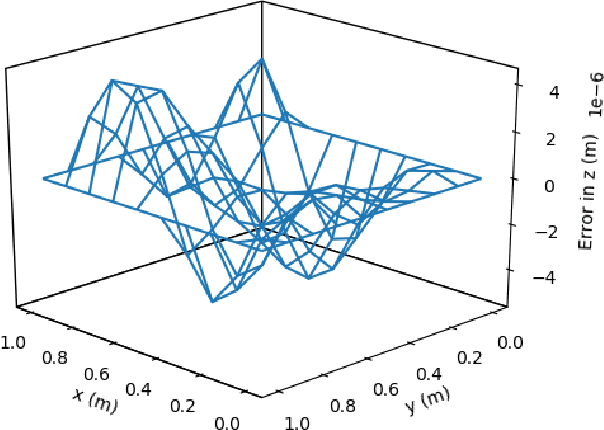
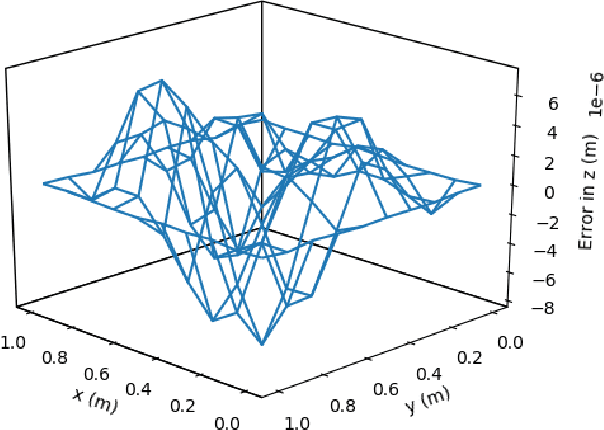
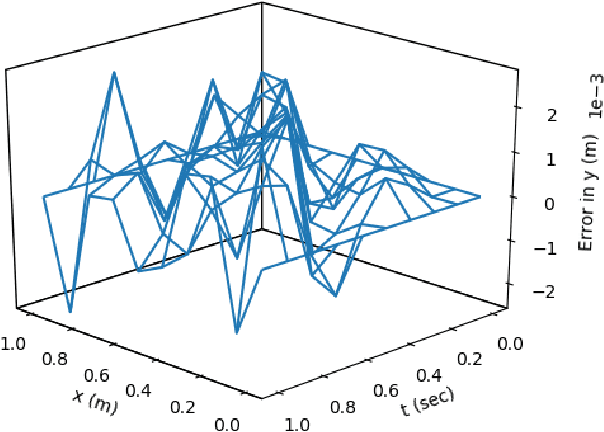
This article presents a new methodology called deep ToC that estimates the solutions of partial differential equations (PDEs) by combining neural networks with the Theory of Connections (ToC). ToC is used to transform PDEs with boundary conditions into unconstrained optimization problems by embedding the boundary conditions into a "constrained expression" that contains a neural network. The loss function for the unconstrained optimization problem is taken to be the square of the residual of the PDE. Then, the neural network is trained in an unsupervised manner to solve the unconstrained optimization problem. This methodology has two major advantages over other popular methods used to estimate the solutions of PDEs. First, this methodology does not need to discretize the domain into a grid, which becomes prohibitive as the dimensionality of the PDE increases. Instead, this methodology randomly samples points from the domain during the training phase. Second, after training, this methodology represents a closed form, analytical, differentiable approximation of the solution throughout the entire training domain. In contrast, other popular methods require interpolation if the estimated solution is desired at points that do not lie on the discretized grid. The deep ToC method for estimating the solution of PDEs is demonstrated on four problems with a variety of boundary conditions.