Planning with Abstract Learned Models While Learning Transferable Subtasks

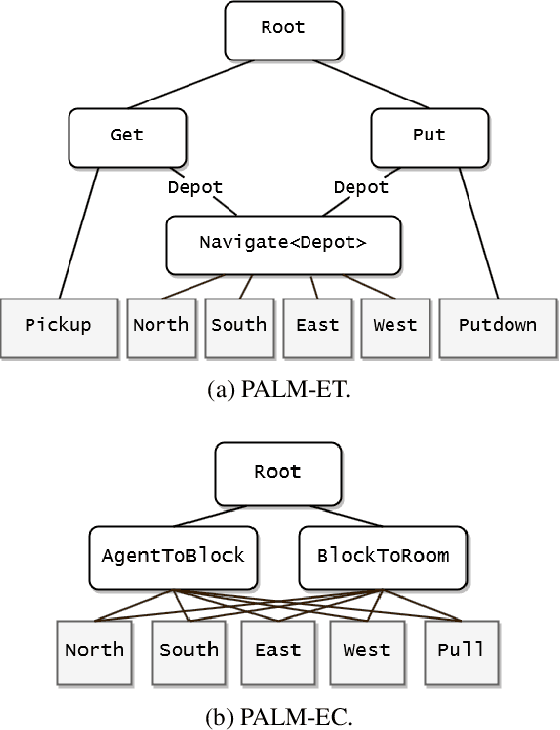
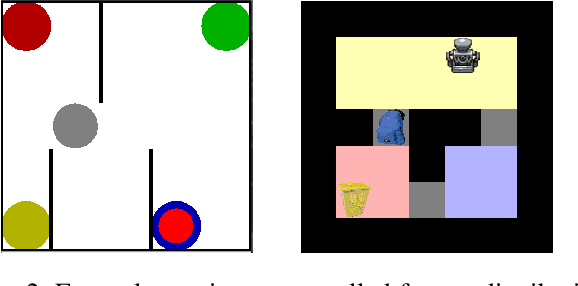
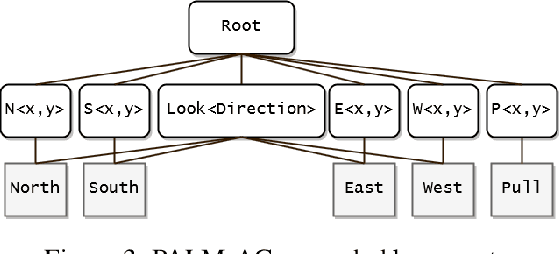
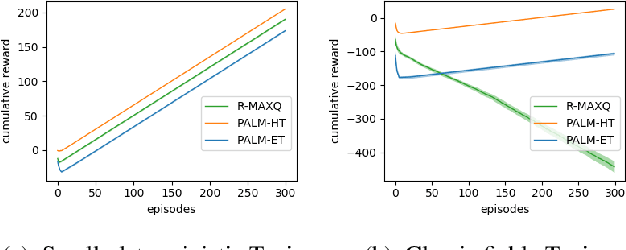
We introduce an algorithm for model-based hierarchical reinforcement learning to acquire self-contained transition and reward models suitable for probabilistic planning at multiple levels of abstraction. We call this framework Planning with Abstract Learned Models (PALM). By representing subtasks symbolically using a new formal structure, the lifted abstract Markov decision process (L-AMDP), PALM learns models that are independent and modular. Through our experiments, we show how PALM integrates planning and execution, facilitating a rapid and efficient learning of abstract, hierarchical models. We also demonstrate the increased potential for learned models to be transferred to new and related tasks.

Representing and Reasoning With Probabilistic Knowledge: A Bayesian Approach

PAGODA (Probabilistic Autonomous Goal-Directed Agent) is a model for autonomous learning in probabilistic domains [desJardins, 1992] that incorporates innovative techniques for using the agent's existing knowledge to guide and constrain the learning process and for representing, reasoning with, and learning probabilistic knowledge. This paper describes the probabilistic representation and inference mechanism used in PAGODA. PAGODA forms theories about the effects of its actions and the world state on the environment over time. These theories are represented as conditional probability distributions. A restriction is imposed on the structure of the theories that allows the inference mechanism to find a unique predicted distribution for any action and world state description. These restricted theories are called uniquely predictive theories. The inference mechanism, Probability Combination using Independence (PCI), uses minimal independence assumptions to combine the probabilities in a theory to make probabilistic predictions.

Multi-view constrained clustering with an incomplete mapping between views

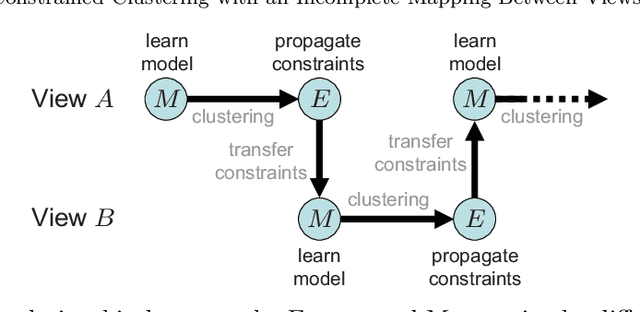
Multi-view learning algorithms typically assume a complete bipartite mapping between the different views in order to exchange information during the learning process. However, many applications provide only a partial mapping between the views, creating a challenge for current methods. To address this problem, we propose a multi-view algorithm based on constrained clustering that can operate with an incomplete mapping. Given a set of pairwise constraints in each view, our approach propagates these constraints using a local similarity measure to those instances that can be mapped to the other views, allowing the propagated constraints to be transferred across views via the partial mapping. It uses co-EM to iteratively estimate the propagation within each view based on the current clustering model, transfer the constraints across views, and then update the clustering model. By alternating the learning process between views, this approach produces a unified clustering model that is consistent with all views. We show that this approach significantly improves clustering performance over several other methods for transferring constraints and allows multi-view clustering to be reliably applied when given a limited mapping between the views. Our evaluation reveals that the propagated constraints have high precision with respect to the true clusters in the data, explaining their benefit to clustering performance in both single- and multi-view learning scenarios.

More-or-Less CP-Networks

Preferences play an important role in our everyday lives. CP-networks, or CP-nets in short, are graphical models for representing conditional qualitative preferences under ceteris paribus ("all else being equal") assumptions. Despite their intuitive nature and rich representation, dominance testing with CP-nets is computationally complex, even when the CP-nets are restricted to binary-valued preferences. Tractable algorithms exist for binary CP-nets, but these algorithms are incomplete for multi-valued CPnets. In this paper, we identify a class of multivalued CP-nets, which we call more-or-less CPnets, that have the same computational complexity as binary CP-nets. More-or-less CP-nets exploit the monotonicity of the attribute values and use intervals to aggregate values that induce similar preferences. We then present a search control rule for dominance testing that effectively prunes the search space while preserving completeness.