Fusun Yaman
More-or-Less CP-Networks
Jun 20, 2012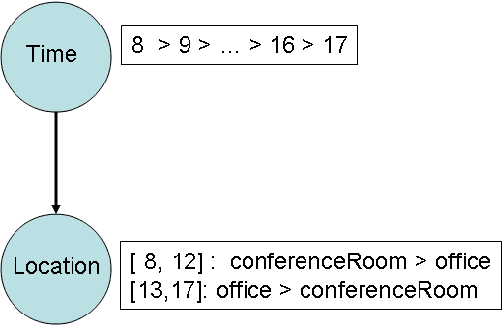



Abstract:Preferences play an important role in our everyday lives. CP-networks, or CP-nets in short, are graphical models for representing conditional qualitative preferences under ceteris paribus ("all else being equal") assumptions. Despite their intuitive nature and rich representation, dominance testing with CP-nets is computationally complex, even when the CP-nets are restricted to binary-valued preferences. Tractable algorithms exist for binary CP-nets, but these algorithms are incomplete for multi-valued CPnets. In this paper, we identify a class of multivalued CP-nets, which we call more-or-less CPnets, that have the same computational complexity as binary CP-nets. More-or-less CP-nets exploit the monotonicity of the attribute values and use intervals to aggregate values that induce similar preferences. We then present a search control rule for dominance testing that effectively prunes the search space while preserving completeness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge