Maria Polukarov
Multi-Agent Reinforcement Learning for Market Making: Competition without Collusion
Oct 29, 2025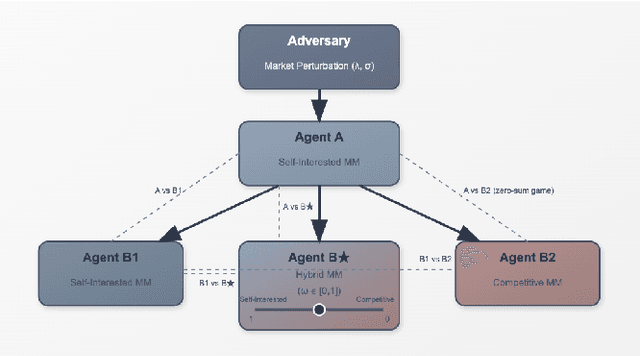



Abstract:Algorithmic collusion has emerged as a central question in AI: Will the interaction between different AI agents deployed in markets lead to collusion? More generally, understanding how emergent behavior, be it a cartel or market dominance from more advanced bots, affects the market overall is an important research question. We propose a hierarchical multi-agent reinforcement learning framework to study algorithmic collusion in market making. The framework includes a self-interested market maker (Agent~A), which is trained in an uncertain environment shaped by an adversary, and three bottom-layer competitors: the self-interested Agent~B1 (whose objective is to maximize its own PnL), the competitive Agent~B2 (whose objective is to minimize the PnL of its opponent), and the hybrid Agent~B$^\star$, which can modulate between the behavior of the other two. To analyze how these agents shape the behavior of each other and affect market outcomes, we propose interaction-level metrics that quantify behavioral asymmetry and system-level dynamics, while providing signals potentially indicative of emergent interaction patterns. Experimental results show that Agent~B2 secures dominant performance in a zero-sum setting against B1, aggressively capturing order flow while tightening average spreads, thus improving market execution efficiency. In contrast, Agent~B$^\star$ exhibits a self-interested inclination when co-existing with other profit-seeking agents, securing dominant market share through adaptive quoting, yet exerting a milder adverse impact on the rewards of Agents~A and B1 compared to B2. These findings suggest that adaptive incentive control supports more sustainable strategic co-existence in heterogeneous agent environments and offers a structured lens for evaluating behavioral design in algorithmic trading systems.
Information Loss in Euclidean Preference Models
Aug 17, 2022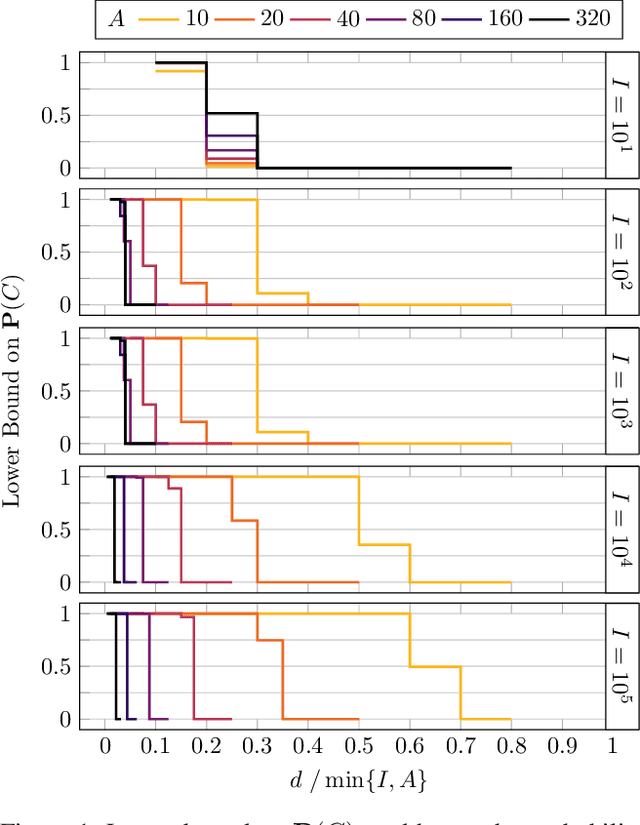
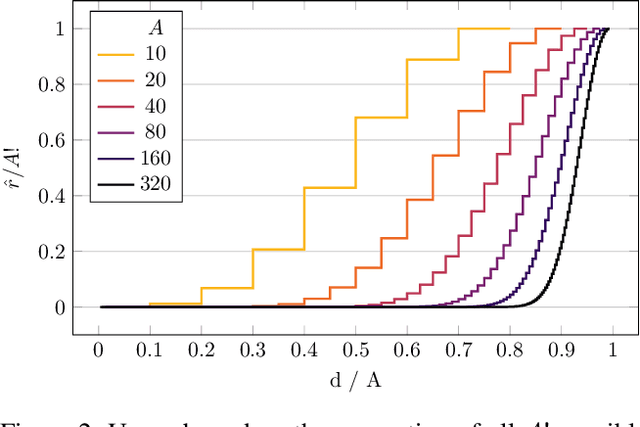
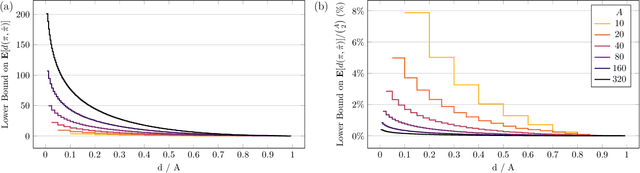
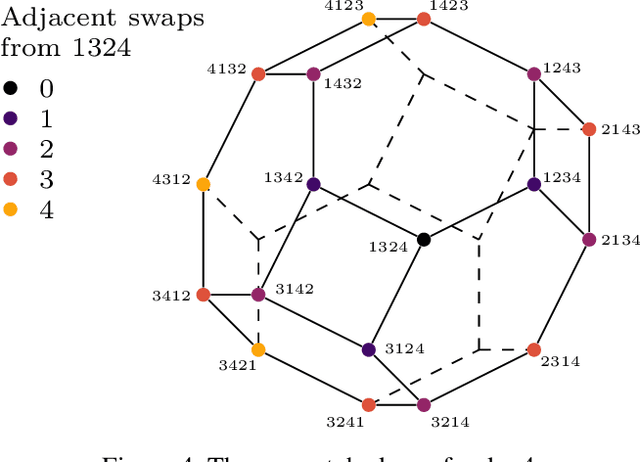
Abstract:Spatial models of preference, in the form of vector embeddings, are learned by many deep learning systems including recommender systems. Often these models are assumed to approximate a Euclidean structure, where an individual prefers alternatives positioned closer to their "ideal point", as measured by the Euclidean metric. However, Bogomolnaia and Laslier (2007) showed that there exist ordinal preference profiles that cannot be represented with this structure if the Euclidean space has two fewer dimensions than there are individuals or alternatives. We extend this result, showing that there are realistic situations in which almost all preference profiles cannot be represented with the Euclidean model, and derive a theoretical lower bound on the information lost when approximating non-representable preferences with the Euclidean model. Our results have implications for the interpretation and use of vector embeddings, because in some cases close approximation of arbitrary, true preferences is possible only if the dimensionality of the embeddings is a substantial fraction of the number of individuals or alternatives.
Denoised Labels for Financial Time-Series Data via Self-Supervised Learning
Dec 19, 2021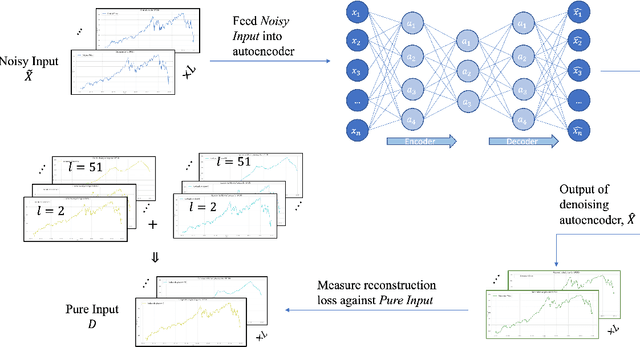
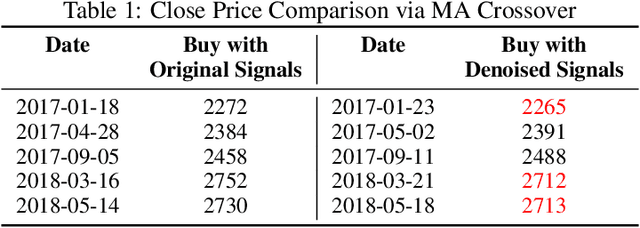
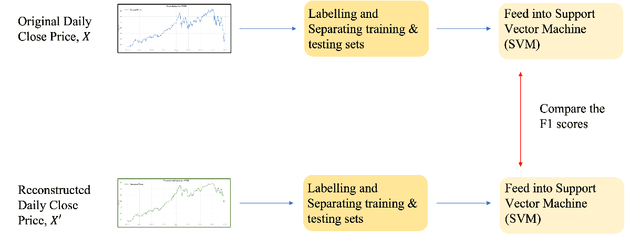

Abstract:The introduction of electronic trading platforms effectively changed the organisation of traditional systemic trading from quote-driven markets into order-driven markets. Its convenience led to an exponentially increasing amount of financial data, which is however hard to use for the prediction of future prices, due to the low signal-to-noise ratio and the non-stationarity of financial time series. Simpler classification tasks -- where the goal is to predict the directions of future price movement -- via supervised learning algorithms, need sufficiently reliable labels to generalise well. Labelling financial data is however less well defined than other domains: did the price go up because of noise or because of signal? The existing labelling methods have limited countermeasures against noise and limited effects in improving learning algorithms. This work takes inspiration from image classification in trading and success in self-supervised learning. We investigate the idea of applying computer vision techniques to financial time-series to reduce the noise exposure and hence generate correct labels. We look at the label generation as the pretext task of a self-supervised learning approach and compare the naive (and noisy) labels, commonly used in the literature, with the labels generated by a denoising autoencoder for the same downstream classification task. Our results show that our denoised labels improve the performances of the downstream learning algorithm, for both small and large datasets. We further show that the signals we obtain can be used to effectively trade with binary strategies. We suggest that with proposed techniques, self-supervised learning constitutes a powerful framework for generating "better" financial labels that are useful for studying the underlying patterns of the market.
New Results on Equilibria in Strategic Candidacy
Feb 24, 2016
Abstract:We consider a voting setting where candidates have preferences about the outcome of the election and are free to join or leave the election. The corresponding candidacy game, where candidates choose strategically to participate or not, has been studied %initially by Dutta et al., who showed that no non-dictatorial voting procedure satisfying unanimity is candidacy-strategyproof, that is, is such that the joint action where all candidates enter the election is always a pure strategy Nash equilibrium. Dutta et al. also showed that for some voting tree procedures, there are candidacy games with no pure Nash equilibria, and that for the rule that outputs the sophisticated winner of voting by successive elimination, all games have a pure Nash equilibrium. No results were known about other voting rules. Here we prove several such results. For four candidates, the message is, roughly, that most scoring rules (with the exception of Borda) do not guarantee the existence of a pure Nash equilibrium but that Condorcet-consistent rules, for an odd number of voters, do. For five candidates, most rules we study no longer have this guarantee. Finally, we identify one prominent rule that guarantees the existence of a pure Nash equilibrium for any number of candidates (and for an odd number of voters): the Copeland rule. We also show that under mild assumptions on the voting rule, the existence of strong equilibria cannot be guaranteed.
Graph Coalition Structure Generation
Feb 08, 2011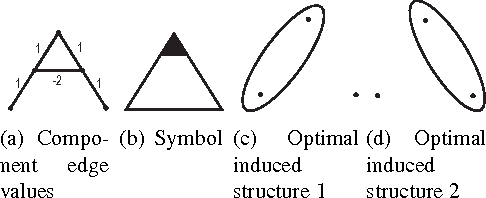
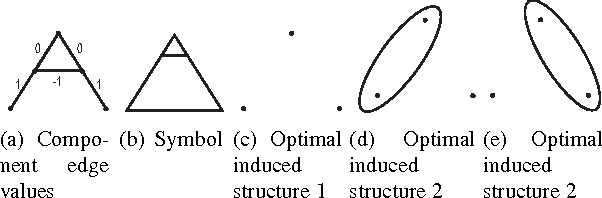
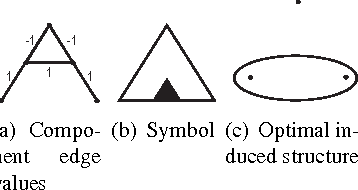

Abstract:We give the first analysis of the computational complexity of {\it coalition structure generation over graphs}. Given an undirected graph $G=(N,E)$ and a valuation function $v:2^N\rightarrow\RR$ over the subsets of nodes, the problem is to find a partition of $N$ into connected subsets, that maximises the sum of the components' values. This problem is generally NP--complete; in particular, it is hard for a defined class of valuation functions which are {\it independent of disconnected members}---that is, two nodes have no effect on each other's marginal contribution to their vertex separator. Nonetheless, for all such functions we provide bounds on the complexity of coalition structure generation over general and minor free graphs. Our proof is constructive and yields algorithms for solving corresponding instances of the problem. Furthermore, we derive polynomial time bounds for acyclic, $K_{2,3}$ and $K_4$ minor free graphs. However, as we show, the problem remains NP--complete for planar graphs, and hence, for any $K_k$ minor free graphs where $k\geq 5$. Moreover, our hardness result holds for a particular subclass of valuation functions, termed {\it edge sum}, where the value of each subset of nodes is simply determined by the sum of given weights of the edges in the induced subgraph.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge