Alice Cohen-Hadria
One or Two Components? The Scattering Transform Answers
Mar 02, 2020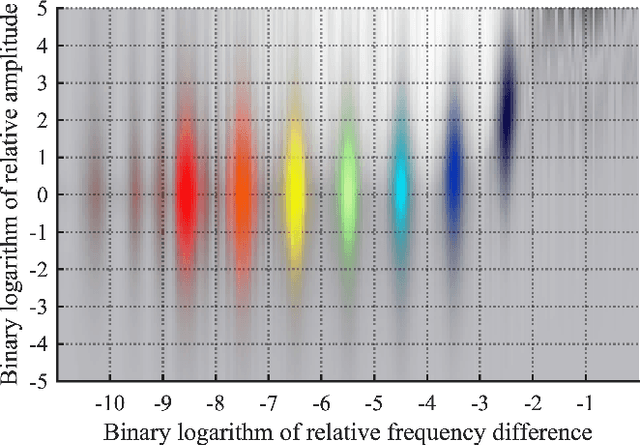
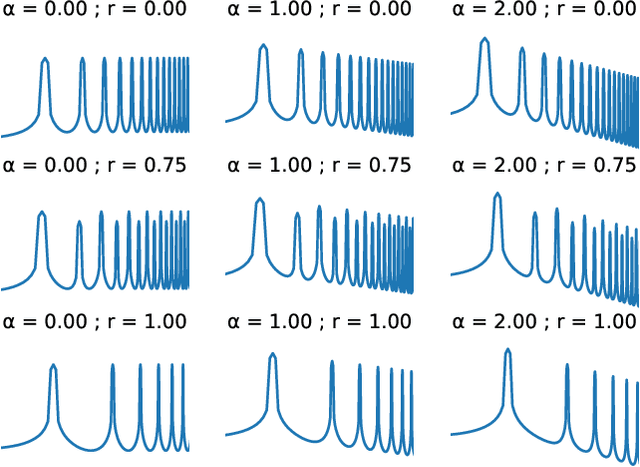
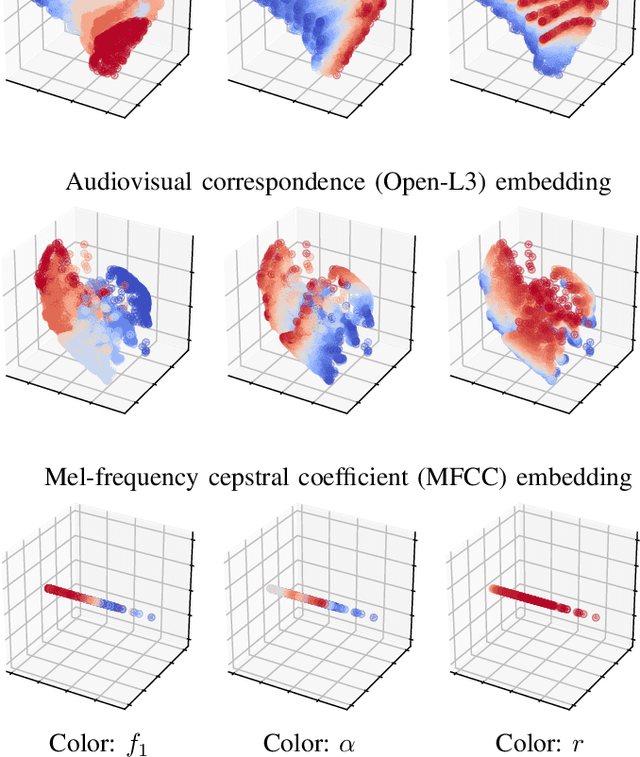
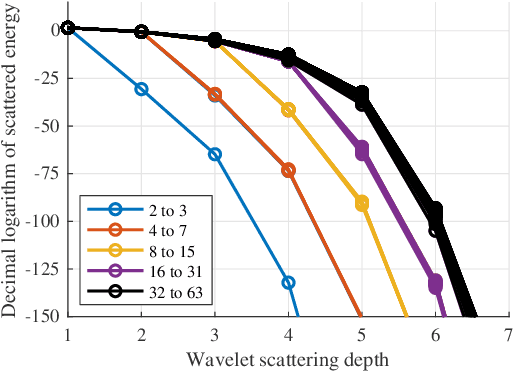
Abstract:With the aim of constructing a biologically plausible model of machine listening, we study the representation of a multicomponent stationary signal by a wavelet scattering network. First, we show that renormalizing second-order nodes by their first-order parents gives a simple numerical criterion to assess whether two neighboring components will interfere psychoacoustically. Secondly, we run a manifold learning algorithm (Isomap) on scattering coefficients to visualize the similarity space underlying parametric additive synthesis. Thirdly, we generalize the "one or two components" framework to three sine waves or more, and prove that the effective scattering depth of a Fourier series grows in logarithmic proportion to its bandwidth.
DALI: a large Dataset of synchronized Audio, LyrIcs and notes, automatically created using teacher-student machine learning paradigm
Jun 25, 2019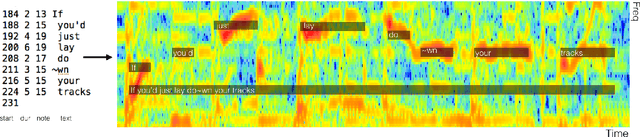


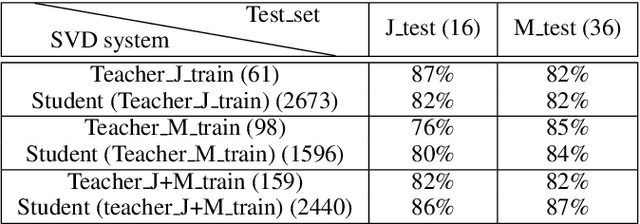
Abstract:The goal of this paper is twofold. First, we introduce DALI, a large and rich multimodal dataset containing 5358 audio tracks with their time-aligned vocal melody notes and lyrics at four levels of granularity. The second goal is to explain our methodology where dataset creation and learning models interact using a teacher-student machine learning paradigm that benefits each other. We start with a set of manual annotations of draft time-aligned lyrics and notes made by non-expert users of Karaoke games. This set comes without audio. Therefore, we need to find the corresponding audio and adapt the annotations to it. To that end, we retrieve audio candidates from the Web. Each candidate is then turned into a singing-voice probability over time using a teacher, a deep convolutional neural network singing-voice detection system (SVD), trained on cleaned data. Comparing the time-aligned lyrics and the singing-voice probability, we detect matches and update the time-alignment lyrics accordingly. From this, we obtain new audio sets. They are then used to train new SVD students used to perform again the above comparison. The process could be repeated iteratively. We show that this allows to progressively improve the performances of our SVD and get better audio-matching and alignment.
New Results on Equilibria in Strategic Candidacy
Feb 24, 2016
Abstract:We consider a voting setting where candidates have preferences about the outcome of the election and are free to join or leave the election. The corresponding candidacy game, where candidates choose strategically to participate or not, has been studied %initially by Dutta et al., who showed that no non-dictatorial voting procedure satisfying unanimity is candidacy-strategyproof, that is, is such that the joint action where all candidates enter the election is always a pure strategy Nash equilibrium. Dutta et al. also showed that for some voting tree procedures, there are candidacy games with no pure Nash equilibria, and that for the rule that outputs the sophisticated winner of voting by successive elimination, all games have a pure Nash equilibrium. No results were known about other voting rules. Here we prove several such results. For four candidates, the message is, roughly, that most scoring rules (with the exception of Borda) do not guarantee the existence of a pure Nash equilibrium but that Condorcet-consistent rules, for an odd number of voters, do. For five candidates, most rules we study no longer have this guarantee. Finally, we identify one prominent rule that guarantees the existence of a pure Nash equilibrium for any number of candidates (and for an odd number of voters): the Copeland rule. We also show that under mild assumptions on the voting rule, the existence of strong equilibria cannot be guaranteed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge