One or Two Components? The Scattering Transform Answers
Paper and Code
Mar 02, 2020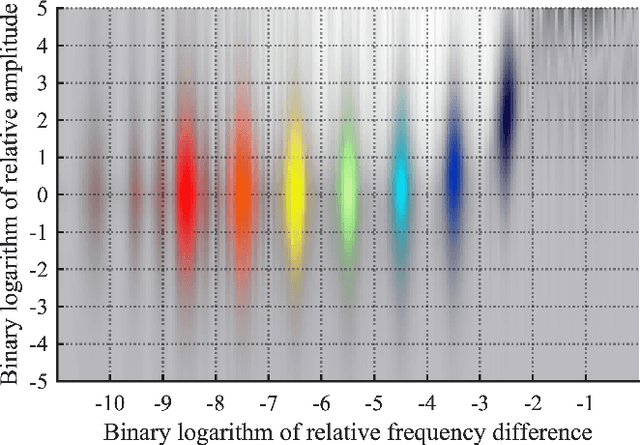
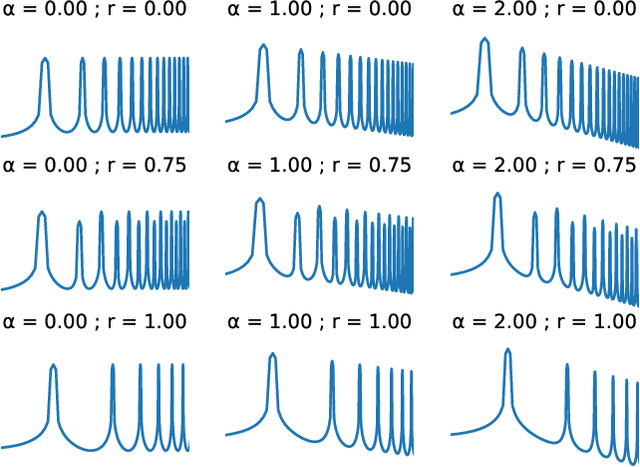
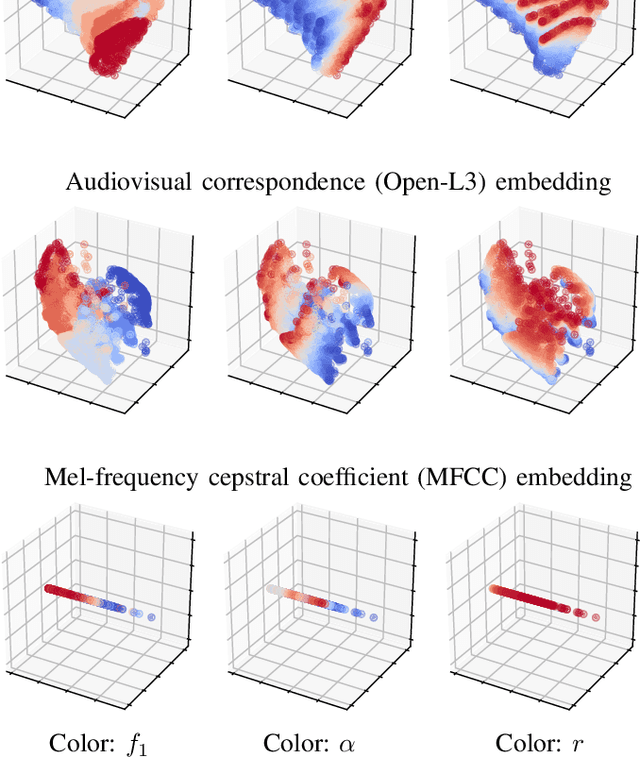
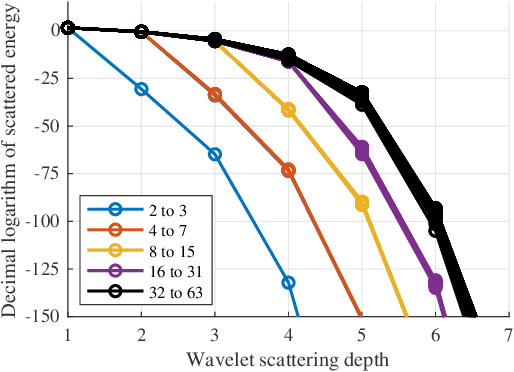
With the aim of constructing a biologically plausible model of machine listening, we study the representation of a multicomponent stationary signal by a wavelet scattering network. First, we show that renormalizing second-order nodes by their first-order parents gives a simple numerical criterion to assess whether two neighboring components will interfere psychoacoustically. Secondly, we run a manifold learning algorithm (Isomap) on scattering coefficients to visualize the similarity space underlying parametric additive synthesis. Thirdly, we generalize the "one or two components" framework to three sine waves or more, and prove that the effective scattering depth of a Fourier series grows in logarithmic proportion to its bandwidth.
* 5 pages, 4 figures, in English. Submitted to the European Signal
Processing Conference (EUSIPCO 2020)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge