An Open-Source Framework for Efficient Numerically-Tailored Computations

We present a versatile open-source framework designed to facilitate efficient, numerically-tailored Matrix-Matrix Multiplications (MMMs). The framework offers two primary contributions: first, a fine-tuned, automated pipeline for arithmetic datapath generation, enabling highly customizable systolic MMM kernels; second, seamless integration of the generated kernels into user code, irrespective of the programming language employed, without necessitating modifications. The framework demonstrates a systematic enhancement in accuracy per energy cost across diverse High Performance Computing (HPC) workloads displaying a variety of numerical requirements, such as Artificial Intelligence (AI) inference and Sea Surface Height (SSH) computation. For AI inference, we consider a set of state-of-the-art neural network models, namely ResNet18, ResNet34, ResNet50, DenseNet121, DenseNet161, DenseNet169, and VGG11, in conjunction with two datasets, two computer formats, and 27 distinct intermediate arithmetic datapaths. Our approach consistently reduces energy consumption across all cases, with a notable example being the reduction by factors of $3.3\times$ for IEEE754-32 and $1.4\times$ for Bfloat16 during ImageNet inference with ResNet50. This is accomplished while maintaining accuracies of $82.3\%$ and $86\%$, comparable to those achieved with conventional Floating-Point Units (FPUs). In the context of SSH computation, our method achieves fully-reproducible results using double-precision words, surpassing the accuracy of conventional double- and quad-precision arithmetic in FPUs. Our approach enhances SSH computation accuracy by a minimum of $5\times$ and $27\times$ compared to IEEE754-64 and IEEE754-128, respectively, resulting in $5.6\times$ and $15.1\times$ improvements in accuracy per power cost.

Compressed Real Numbers for AI: a case-study using a RISC-V CPU

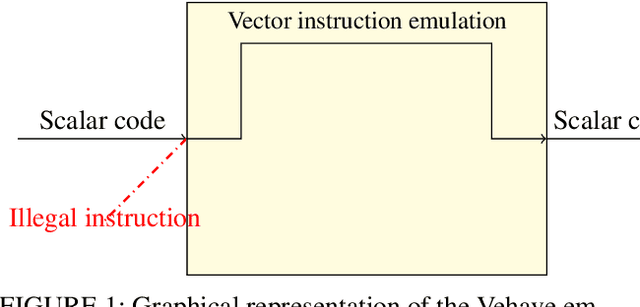
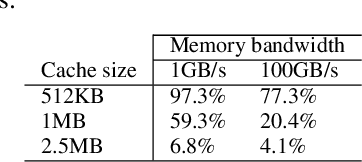
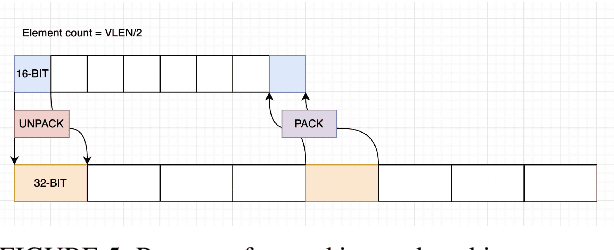
As recently demonstrated, Deep Neural Networks (DNN), usually trained using single precision IEEE 754 floating point numbers (binary32), can also work using lower precision. Therefore, 16-bit and 8-bit compressed format have attracted considerable attention. In this paper, we focused on two families of formats that have already achieved interesting results in compressing binary32 numbers in machine learning applications, without sensible degradation of the accuracy: bfloat and posit. Even if 16-bit and 8-bit bfloat/posit are routinely used for reducing the storage of the weights/biases of trained DNNs, the inference still often happens on the 32-bit FPU of the CPU (especially if GPUs are not available). In this paper we propose a way to decompress a tensor of bfloat/posits just before computations, i.e., after the compressed operands have been loaded within the vector registers of a vector capable CPU, in order to save bandwidth usage and increase cache efficiency. Finally, we show the architectural parameters and considerations under which this solution is advantageous with respect to the uncompressed one.

Generating Efficient DNN-Ensembles with Evolutionary Computation

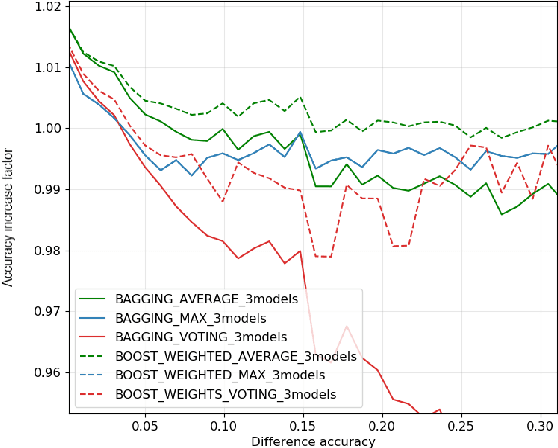
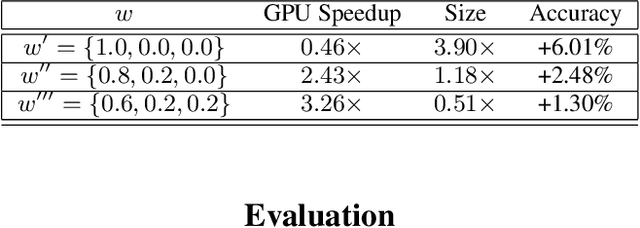
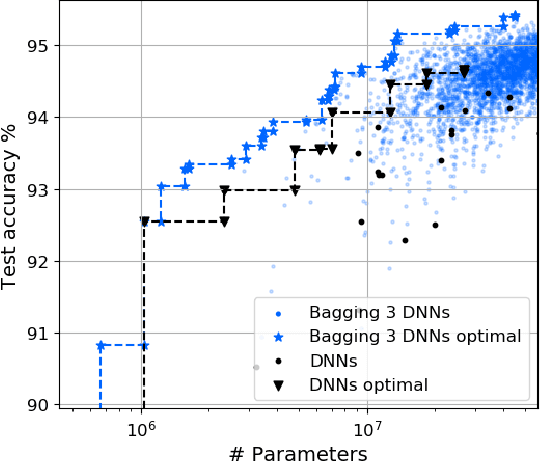
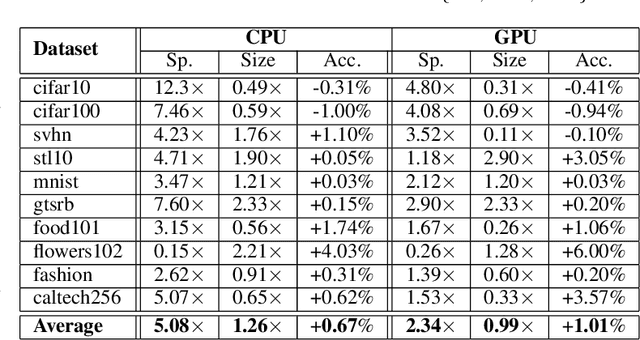
In this work, we leverage ensemble learning as a tool for the creation of faster, smaller, and more accurate deep learning models. We demonstrate that we can jointly optimize for accuracy, inference time, and the number of parameters by combining DNN classifiers. To achieve this, we combine multiple ensemble strategies: bagging, boosting, and an ordered chain of classifiers. To reduce the number of DNN ensemble evaluations during the search, we propose EARN, an evolutionary approach that optimizes the ensemble according to three objectives regarding the constraints specified by the user. We run EARN on 10 image classification datasets with an initial pool of 32 state-of-the-art DCNN on both CPU and GPU platforms, and we generate models with speedups up to $7.60\times$, reductions of parameters by $10\times$, or increases in accuracy up to $6.01\%$ regarding the best DNN in the pool. In addition, our method generates models that are $5.6\times$ faster than the state-of-the-art methods for automatic model generation.

Low-Precision Floating-Point Schemes for Neural Network Training

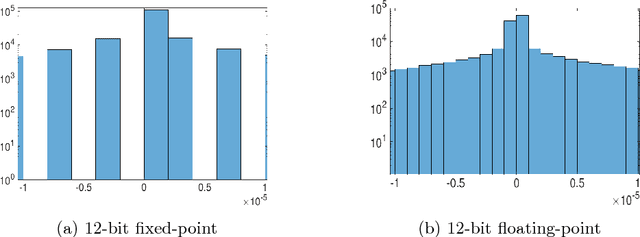
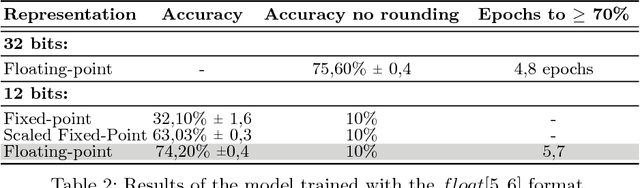
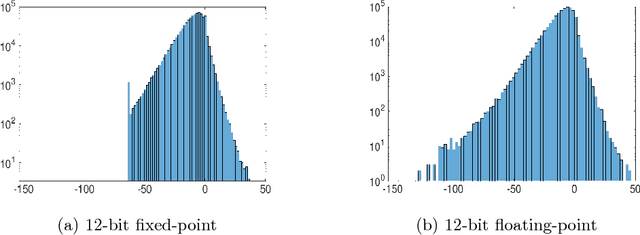
The use of low-precision fixed-point arithmetic along with stochastic rounding has been proposed as a promising alternative to the commonly used 32-bit floating point arithmetic to enhance training neural networks training in terms of performance and energy efficiency. In the first part of this paper, the behaviour of the 12-bit fixed-point arithmetic when training a convolutional neural network with the CIFAR-10 dataset is analysed, showing that such arithmetic is not the most appropriate for the training phase. After that, the paper presents and evaluates, under the same conditions, alternative low-precision arithmetics, starting with the 12-bit floating-point arithmetic. These two representations are then leveraged using local scaling in order to increase accuracy and get closer to the baseline 32-bit floating-point arithmetic. Finally, the paper introduces a simplified model in which both the outputs and the gradients of the neural networks are constrained to power-of-two values, just using 7 bits for their representation. The evaluation demonstrates a minimal loss in accuracy for the proposed Power-of-Two neural network, avoiding the use of multiplications and divisions and thereby, significantly reducing the training time as well as the energy consumption and memory requirements during the training and inference phases.