FinRobot: An Open-Source AI Agent Platform for Financial Applications using Large Language Models

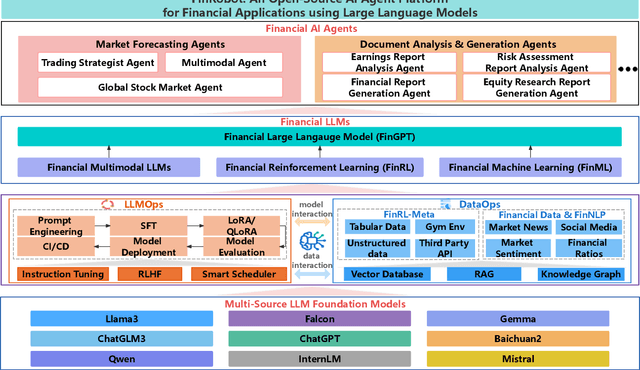
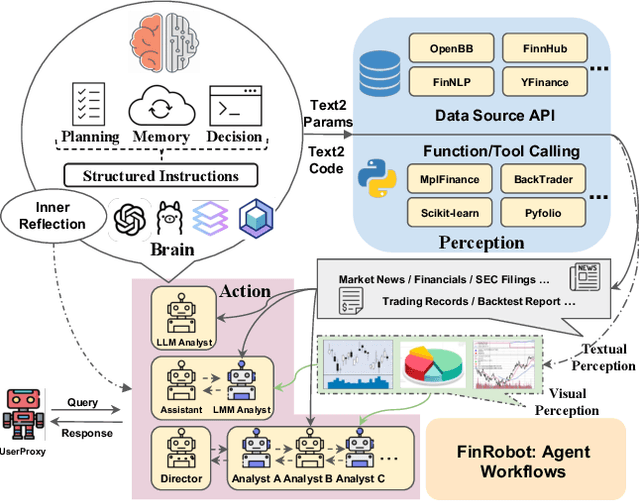
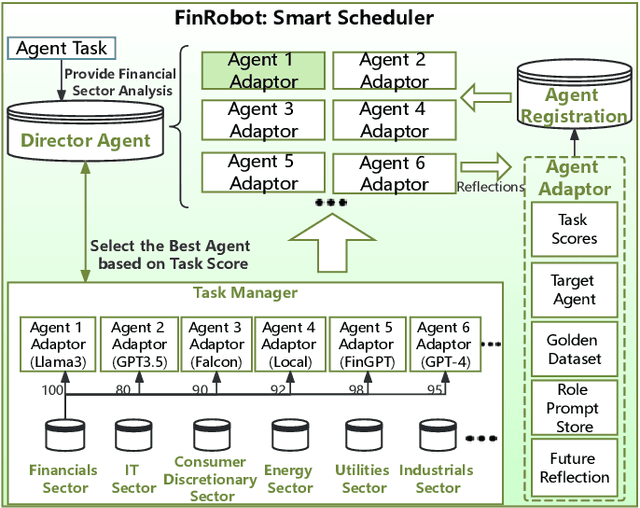
As financial institutions and professionals increasingly incorporate Large Language Models (LLMs) into their workflows, substantial barriers, including proprietary data and specialized knowledge, persist between the finance sector and the AI community. These challenges impede the AI community's ability to enhance financial tasks effectively. Acknowledging financial analysis's critical role, we aim to devise financial-specialized LLM-based toolchains and democratize access to them through open-source initiatives, promoting wider AI adoption in financial decision-making. In this paper, we introduce FinRobot, a novel open-source AI agent platform supporting multiple financially specialized AI agents, each powered by LLM. Specifically, the platform consists of four major layers: 1) the Financial AI Agents layer that formulates Financial Chain-of-Thought (CoT) by breaking sophisticated financial problems down into logical sequences; 2) the Financial LLM Algorithms layer dynamically configures appropriate model application strategies for specific tasks; 3) the LLMOps and DataOps layer produces accurate models by applying training/fine-tuning techniques and using task-relevant data; 4) the Multi-source LLM Foundation Models layer that integrates various LLMs and enables the above layers to access them directly. Finally, FinRobot provides hands-on for both professional-grade analysts and laypersons to utilize powerful AI techniques for advanced financial analysis. We open-source FinRobot at \url{https://github.com/AI4Finance-Foundation/FinRobot}.

Explainable Deep Reinforcement Learning for Portfolio Management: An Empirical Approach

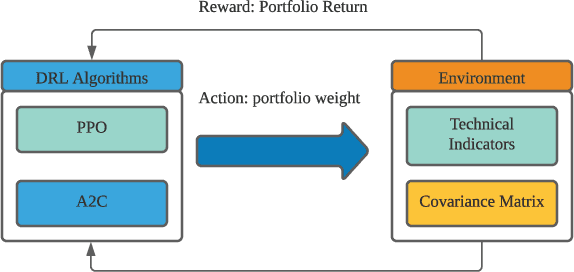
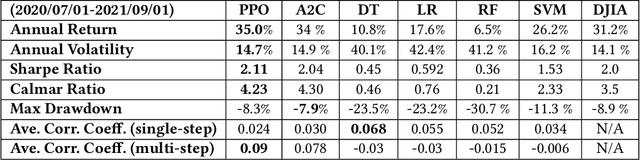
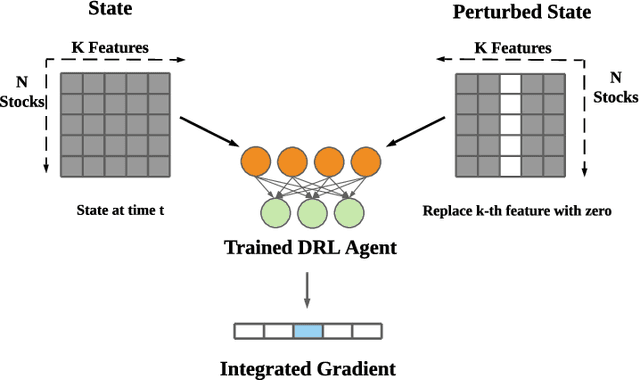
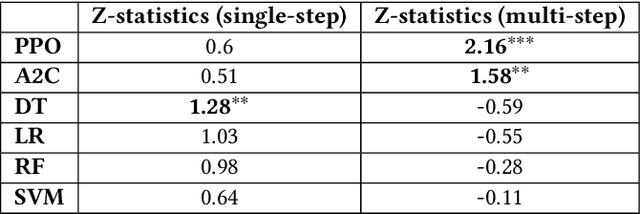
Deep reinforcement learning (DRL) has been widely studied in the portfolio management task. However, it is challenging to understand a DRL-based trading strategy because of the black-box nature of deep neural networks. In this paper, we propose an empirical approach to explain the strategies of DRL agents for the portfolio management task. First, we use a linear model in hindsight as the reference model, which finds the best portfolio weights by assuming knowing actual stock returns in foresight. In particular, we use the coefficients of a linear model in hindsight as the reference feature weights. Secondly, for DRL agents, we use integrated gradients to define the feature weights, which are the coefficients between reward and features under a linear regression model. Thirdly, we study the prediction power in two cases, single-step prediction and multi-step prediction. In particular, we quantify the prediction power by calculating the linear correlations between the feature weights of a DRL agent and the reference feature weights, and similarly for machine learning methods. Finally, we evaluate a portfolio management task on Dow Jones 30 constituent stocks during 01/01/2009 to 09/01/2021. Our approach empirically reveals that a DRL agent exhibits a stronger multi-step prediction power than machine learning methods.