Superintelligence cannot be contained: Lessons from Computability Theory

Superintelligence is a hypothetical agent that possesses intelligence far surpassing that of the brightest and most gifted human minds. In light of recent advances in machine intelligence, a number of scientists, philosophers and technologists have revived the discussion about the potential catastrophic risks entailed by such an entity. In this article, we trace the origins and development of the neo-fear of superintelligence, and some of the major proposals for its containment. We argue that such containment is, in principle, impossible, due to fundamental limits inherent to computing itself. Assuming that a superintelligence will contain a program that includes all the programs that can be executed by a universal Turing machine on input potentially as complex as the state of the world, strict containment requires simulations of such a program, something theoretically (and practically) infeasible.

Is the Multiverse Hypothesis capable of explaining the Fine Tuning of Nature Laws and Constants? The Case of Cellular Automata

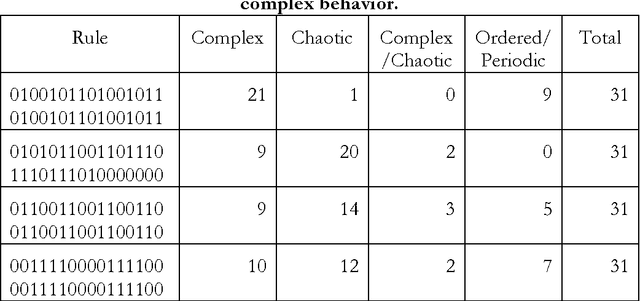
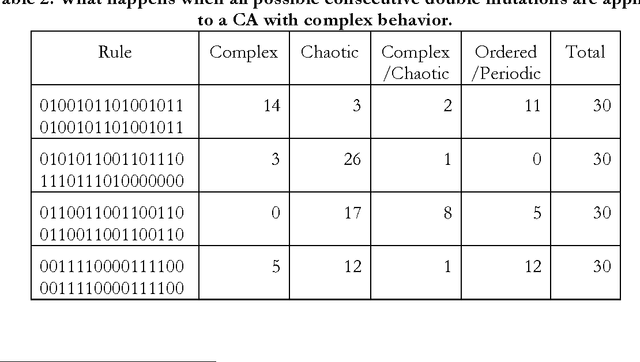
The objective of this paper is analyzing to which extent the multiverse hypothesis provides a real explanation of the peculiarities of the laws and constants in our universe. First we argue in favor of the thesis that all multiverses except Tegmark's <<mathematical multiverse>> are too small to explain the fine tuning, so that they merely shift the problem up one level. But the <<mathematical multiverse>> is surely too large. To prove this assessment, we have performed a number of experiments with cellular automata of complex behavior, which can be considered as universes in the mathematical multiverse. The analogy between what happens in some automata (in particular Conway's <<Game of Life>>) and the real world is very strong. But if the results of our experiments can be extrapolated to our universe, we should expect to inhabit -- in the context of the multiverse -- a world in which at least some of the laws and constants of nature should show a certain time dependence. Actually, the probability of our existence in a world such as ours would be mathematically equal to zero. In consequence, the results presented in this paper can be considered as an inkling that the hypothesis of the multiverse, whatever its type, does not offer an adequate explanation for the peculiarities of the physical laws in our world. A slightly reduced version of this paper has been published in the Journal for General Philosophy of Science, Springer, March 2013, DOI: 10.1007/s10838-013-9215-7.

Overcoming Problems in the Measurement of Biological Complexity

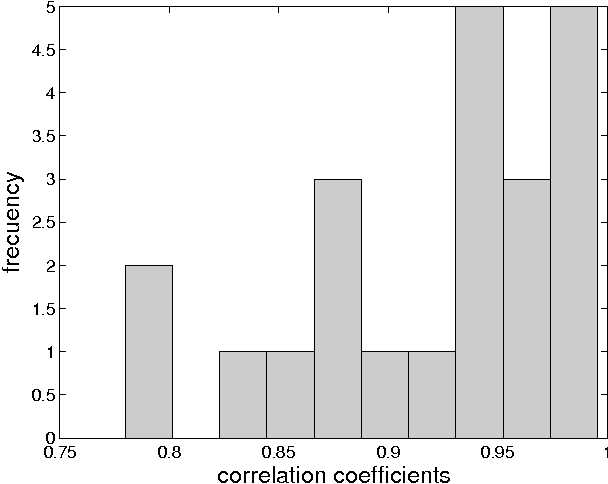
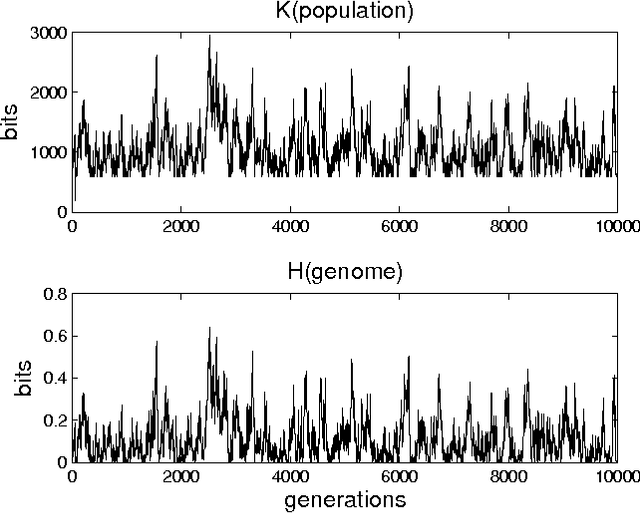
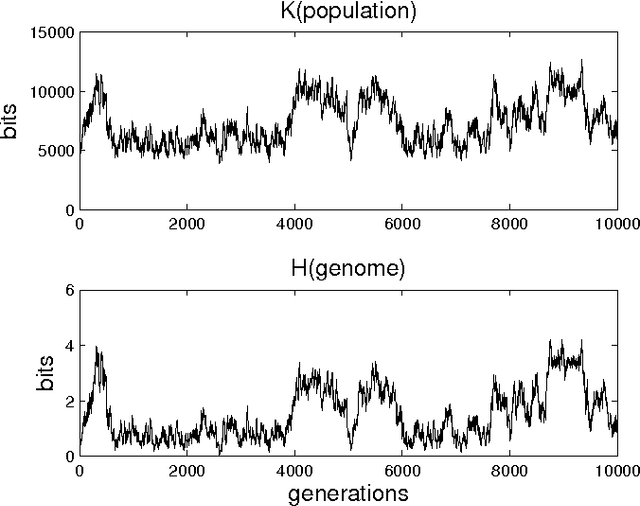
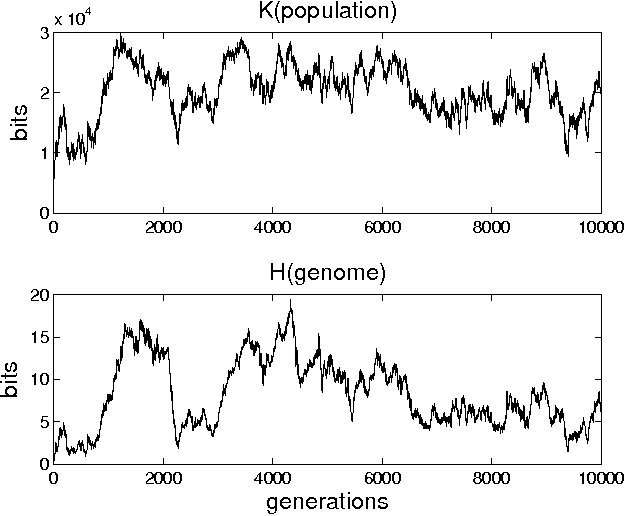
In a genetic algorithm, fluctuations of the entropy of a genome over time are interpreted as fluctuations of the information that the genome's organism is storing about its environment, being this reflected in more complex organisms. The computation of this entropy presents technical problems due to the small population sizes used in practice. In this work we propose and test an alternative way of measuring the entropy variation in a population by means of algorithmic information theory, where the entropy variation between two generational steps is the Kolmogorov complexity of the first step conditioned to the second one. As an example application of this technique, we report experimental differences in entropy evolution between systems in which sexual reproduction is present or absent.

Grammatical Evolution with Restarts for Fast Fractal Generation

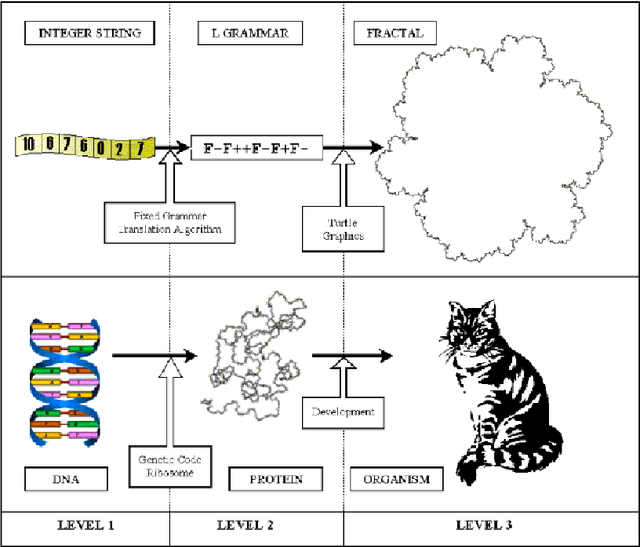
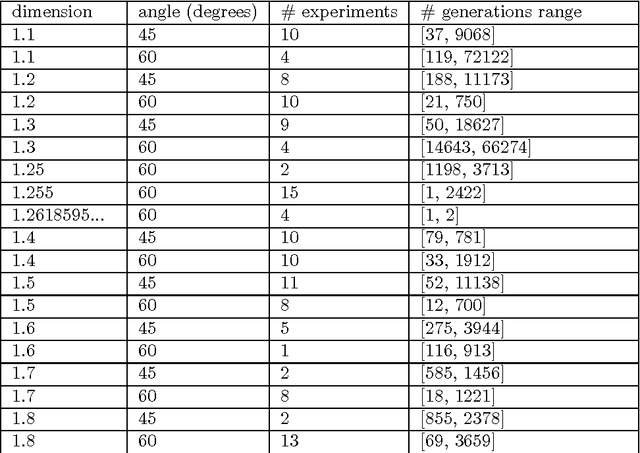
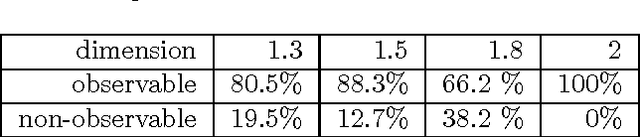
In a previous work, the authors proposed a Grammatical Evolution algorithm to automatically generate Lindenmayer Systems which represent fractal curves with a pre-determined fractal dimension. This paper gives strong statistical evidence that the probability distributions of the execution time of that algorithm exhibits a heavy tail with an hyperbolic probability decay for long executions, which explains the erratic performance of different executions of the algorithm. Three different restart strategies have been incorporated in the algorithm to mitigate the problems associated to heavy tail distributions: the first assumes full knowledge of the execution time probability distribution, the second and third assume no knowledge. These strategies exploit the fact that the probability of finding a solution in short executions is non-negligible and yield a severe reduction, both in the expected execution time (up to one order of magnitude) and in its variance, which is reduced from an infinite to a finite value.

Automatic Generation of Benchmarks for Plagiarism Detection Tools using Grammatical Evolution

This paper has been withdrawn by the authors due to a major rewriting.