Grammatical Evolution with Restarts for Fast Fractal Generation
Paper and Code
Oct 15, 2010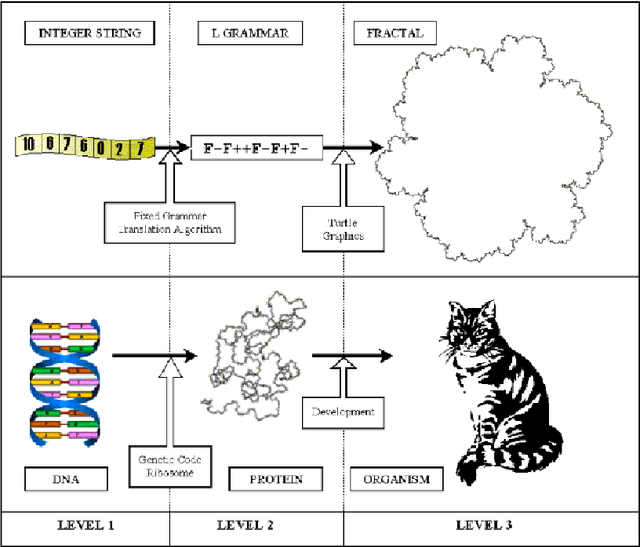
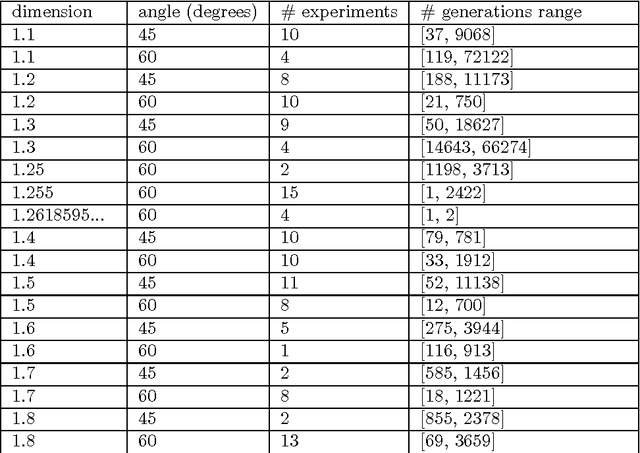

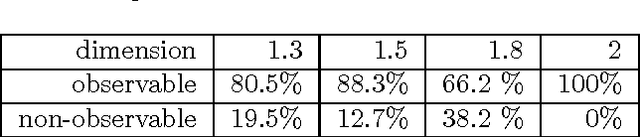
In a previous work, the authors proposed a Grammatical Evolution algorithm to automatically generate Lindenmayer Systems which represent fractal curves with a pre-determined fractal dimension. This paper gives strong statistical evidence that the probability distributions of the execution time of that algorithm exhibits a heavy tail with an hyperbolic probability decay for long executions, which explains the erratic performance of different executions of the algorithm. Three different restart strategies have been incorporated in the algorithm to mitigate the problems associated to heavy tail distributions: the first assumes full knowledge of the execution time probability distribution, the second and third assume no knowledge. These strategies exploit the fact that the probability of finding a solution in short executions is non-negligible and yield a severe reduction, both in the expected execution time (up to one order of magnitude) and in its variance, which is reduced from an infinite to a finite value.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge