Autonomous Learning of Generative Models with Chemical Reaction Network Ensembles

Can a micron sized sack of interacting molecules autonomously learn an internal model of a complex and fluctuating environment? We draw insights from control theory, machine learning theory, chemical reaction network theory, and statistical physics to develop a general architecture whereby a broad class of chemical systems can autonomously learn complex distributions. Our construction takes the form of a chemical implementation of machine learning's optimization workhorse: gradient descent on the relative entropy cost function. We show how this method can be applied to optimize any detailed balanced chemical reaction network and that the construction is capable of using hidden units to learn complex distributions. This result is then recast as a form of integral feedback control. Finally, due to our use of an explicit physical model of learning, we are able to derive thermodynamic costs and trade-offs associated to this process.

Detailed Balanced Chemical Reaction Networks as Generalized Boltzmann Machines

Can a micron sized sack of interacting molecules understand, and adapt to a constantly-fluctuating environment? Cellular life provides an existence proof in the affirmative, but the principles that allow for life's existence are far from being proven. One challenge in engineering and understanding biochemical computation is the intrinsic noise due to chemical fluctuations. In this paper, we draw insights from machine learning theory, chemical reaction network theory, and statistical physics to show that the broad and biologically relevant class of detailed balanced chemical reaction networks is capable of representing and conditioning complex distributions. These results illustrate how a biochemical computer can use intrinsic chemical noise to perform complex computations. Furthermore, we use our explicit physical model to derive thermodynamic costs of inference.

Active Inference for Stochastic Control

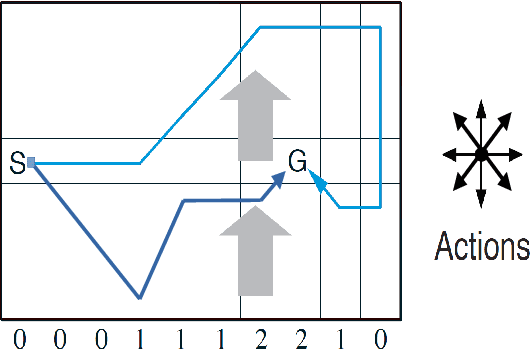
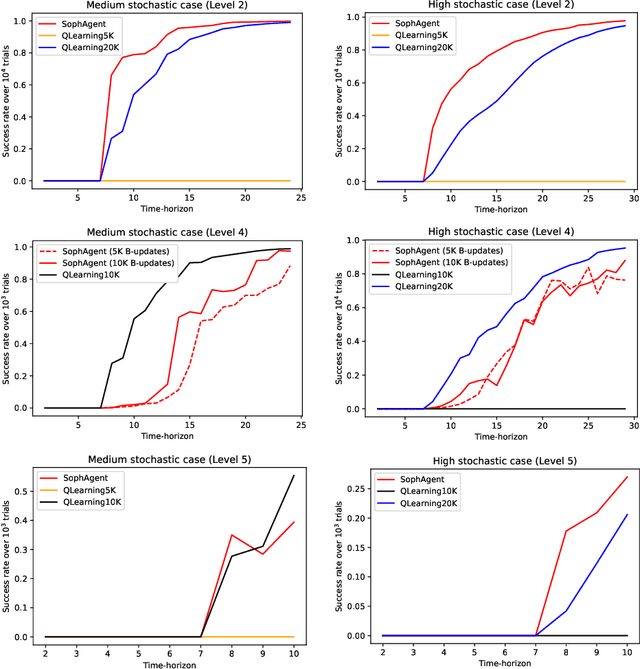
Active inference has emerged as an alternative approach to control problems given its intuitive (probabilistic) formalism. However, despite its theoretical utility, computational implementations have largely been restricted to low-dimensional, deterministic settings. This paper highlights that this is a consequence of the inability to adequately model stochastic transition dynamics, particularly when an extensive policy (i.e., action trajectory) space must be evaluated during planning. Fortunately, recent advancements propose a modified planning algorithm for finite temporal horizons. We build upon this work to assess the utility of active inference for a stochastic control setting. For this, we simulate the classic windy grid-world task with additional complexities, namely: 1) environment stochasticity; 2) learning of transition dynamics; and 3) partial observability. Our results demonstrate the advantage of using active inference, compared to reinforcement learning, in both deterministic and stochastic settings.

A reaction network scheme which implements inference and learning for Hidden Markov Models

With a view towards molecular communication systems and molecular multi-agent systems, we propose the Chemical Baum-Welch Algorithm, a novel reaction network scheme that learns parameters for Hidden Markov Models (HMMs). Each reaction in our scheme changes only one molecule of one species to one molecule of another. The reverse change is also accessible but via a different set of enzymes, in a design reminiscent of futile cycles in biochemical pathways. We show that every fixed point of the Baum-Welch algorithm for HMMs is a fixed point of our reaction network scheme, and every positive fixed point of our scheme is a fixed point of the Baum-Welch algorithm. We prove that the "Expectation" step and the "Maximization" step of our reaction network separately converge exponentially fast. We simulate mass-action kinetics for our network on an example sequence, and show that it learns the same parameters for the HMM as the Baum-Welch algorithm.

A Scheme for Molecular Computation of Maximum Likelihood Estimators for Log-Linear Models

We propose a novel molecular computing scheme for statistical inference. We focus on the much-studied statistical inference problem of computing maximum likelihood estimators for log-linear models. Our scheme takes log-linear models to reaction systems, and the observed data to initial conditions, so that the corresponding equilibrium of each reaction system encodes the corresponding maximum likelihood estimator. The main idea is to exploit the coincidence between thermodynamic entropy and statistical entropy. We map a Maximum Entropy characterization of the maximum likelihood estimator onto a Maximum Entropy characterization of the equilibrium concentrations for the reaction system. This allows for an efficient encoding of the problem, and reveals that reaction networks are superbly suited to statistical inference tasks. Such a scheme may also provide a template to understanding how in vivo biochemical signaling pathways integrate extensive information about their environment and history.