Pattern recognition in the nucleation kinetics of non-equilibrium self-assembly

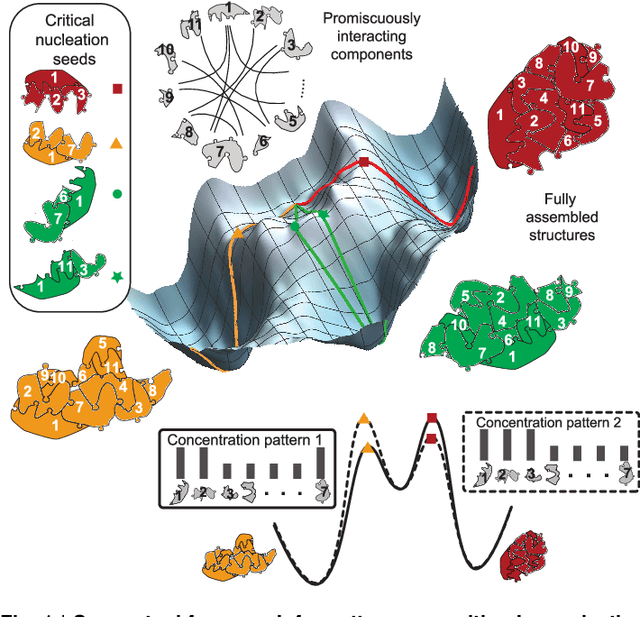
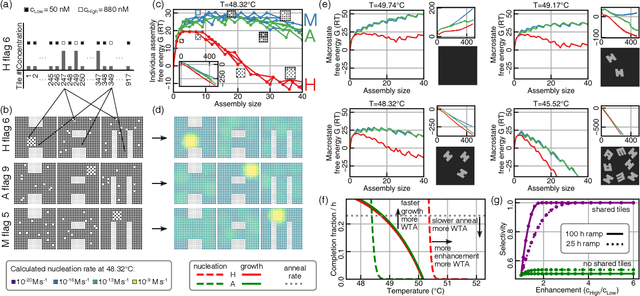
Inspired by biology's most sophisticated computer, the brain, neural networks constitute a profound reformulation of computational principles. Remarkably, analogous high-dimensional, highly-interconnected computational architectures also arise within information-processing molecular systems inside living cells, such as signal transduction cascades and genetic regulatory networks. Might neuromorphic collective modes be found more broadly in other physical and chemical processes, even those that ostensibly play non-information-processing roles such as protein synthesis, metabolism, or structural self-assembly? Here we examine nucleation during self-assembly of multicomponent structures, showing that high-dimensional patterns of concentrations can be discriminated and classified in a manner similar to neural network computation. Specifically, we design a set of 917 DNA tiles that can self-assemble in three alternative ways such that competitive nucleation depends sensitively on the extent of co-localization of high-concentration tiles within the three structures. The system was trained in-silico to classify a set of 18 grayscale 30 x 30 pixel images into three categories. Experimentally, fluorescence and atomic force microscopy monitoring during and after a 150-hour anneal established that all trained images were correctly classified, while a test set of image variations probed the robustness of the results. While slow compared to prior biochemical neural networks, our approach is surprisingly compact, robust, and scalable. This success suggests that ubiquitous physical phenomena, such as nucleation, may hold powerful information processing capabilities when scaled up as high-dimensional multicomponent systems.

Detailed Balanced Chemical Reaction Networks as Generalized Boltzmann Machines

Can a micron sized sack of interacting molecules understand, and adapt to a constantly-fluctuating environment? Cellular life provides an existence proof in the affirmative, but the principles that allow for life's existence are far from being proven. One challenge in engineering and understanding biochemical computation is the intrinsic noise due to chemical fluctuations. In this paper, we draw insights from machine learning theory, chemical reaction network theory, and statistical physics to show that the broad and biologically relevant class of detailed balanced chemical reaction networks is capable of representing and conditioning complex distributions. These results illustrate how a biochemical computer can use intrinsic chemical noise to perform complex computations. Furthermore, we use our explicit physical model to derive thermodynamic costs of inference.