mGNN: Generalizing the Graph Neural Networks to the Multilayer Case

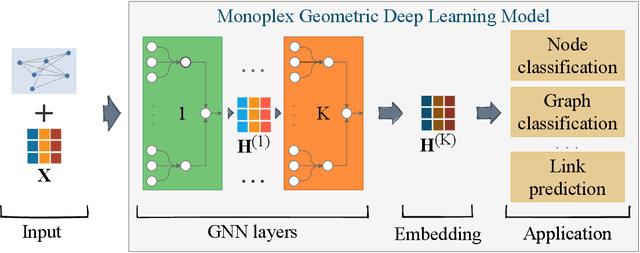
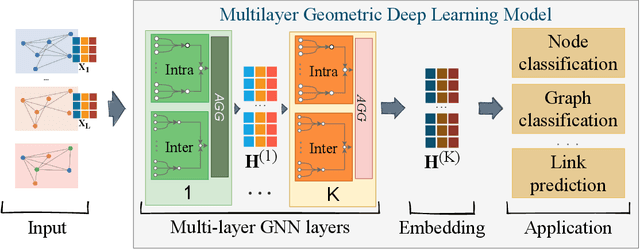
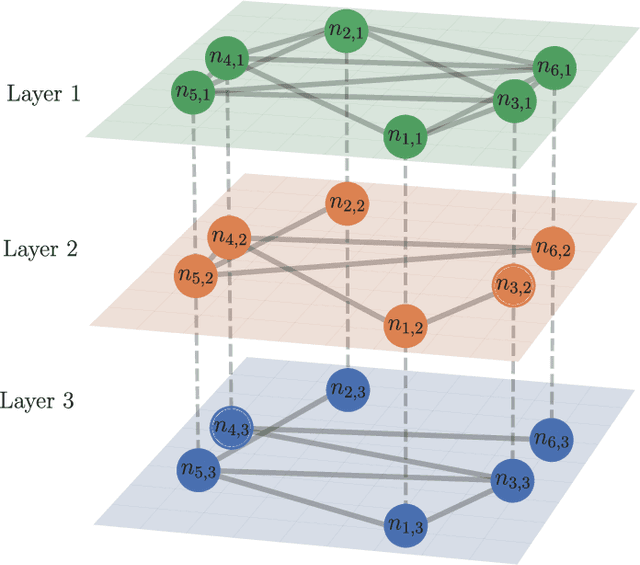
Networks are a powerful tool to model complex systems, and the definition of many Graph Neural Networks (GNN), Deep Learning algorithms that can handle networks, has opened a new way to approach many real-world problems that would be hardly or even untractable. In this paper, we propose mGNN, a framework meant to generalize GNNs to the case of multi-layer networks, i.e., networks that can model multiple kinds of interactions and relations between nodes. Our approach is general (i.e., not task specific) and has the advantage of extending any type of GNN without any computational overhead. We test the framework into three different tasks (node and network classification, link prediction) to validate it.

Machine learning dismantling and early-warning signals of disintegration in complex systems

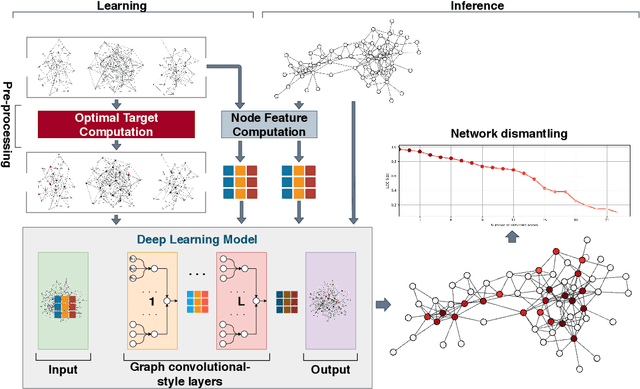
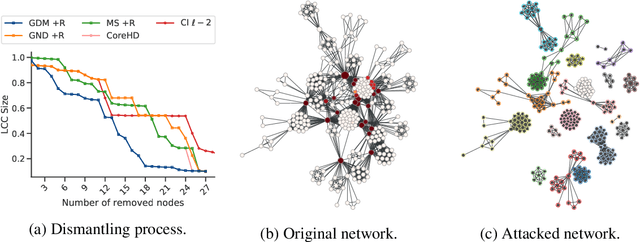
From physics to engineering, biology and social science, natural and artificial systems are characterized by interconnected topologies whose features - e.g., heterogeneous connectivity, mesoscale organization, hierarchy - affect their robustness to external perturbations, such as targeted attacks to their units. Identifying the minimal set of units to attack to disintegrate a complex network, i.e. network dismantling, is a computationally challenging (NP-hard) problem which is usually attacked with heuristics. Here, we show that a machine trained to dismantle relatively small systems is able to identify higher-order topological patterns, allowing to disintegrate large-scale social, infrastructural and technological networks more efficiently than human-based heuristics. Remarkably, the machine assesses the probability that next attacks will disintegrate the system, providing a quantitative method to quantify systemic risk and detect early-warning signals of system's collapse. This demonstrates that machine-assisted analysis can be effectively used for policy and decision making to better quantify the fragility of complex systems and their response to shocks.

Distance entropy cartography characterises centrality in complex networks

We introduce distance entropy as a measure of homogeneity in the distribution of path lengths between a given node and its neighbours in a complex network. Distance entropy defines a new centrality measure whose properties are investigated for a variety of synthetic network models. By coupling distance entropy information with closeness centrality, we introduce a network cartography which allows one to reduce the degeneracy of ranking based on closeness alone. We apply this methodology to the empirical multiplex lexical network encoding the linguistic relationships known to English speaking toddlers. We show that the distance entropy cartography better predicts how children learn words compared to closeness centrality. Our results highlight the importance of distance entropy for gaining insights from distance patterns in complex networks.

Multiplex model of mental lexicon reveals explosive learning in humans

Word similarities affect language acquisition and use in a multi-relational way barely accounted for in the literature. We propose a multiplex network representation of this mental lexicon of word similarities as a natural framework for investigating large-scale cognitive patterns. Our representation accounts for semantic, taxonomic, and phonological interactions and it identifies a cluster of words which are used with greater frequency, are identified, memorised, and learned more easily, and have more meanings than expected at random. This cluster emerges around age 7 through an explosive transition not reproduced by null models. We relate this explosive emergence to polysemy -- redundancy in word meanings. Results indicate that the word cluster acts as a core for the lexicon, increasing both lexical navigability and robustness to linguistic degradation. Our findings provide quantitative confirmation of existing conjectures about core structure in the mental lexicon and the importance of integrating multi-relational word-word interactions in psycholinguistic frameworks.

Convolutional neural networks for structured omics: OmicsCNN and the OmicsConv layer

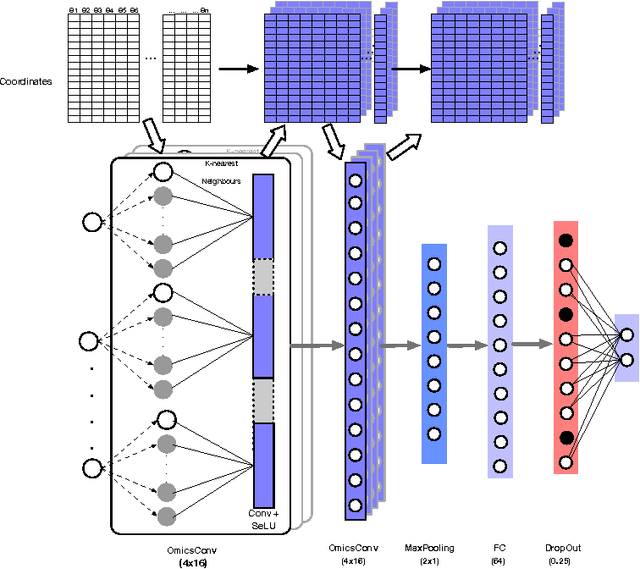
Convolutional Neural Networks (CNNs) are a popular deep learning architecture widely applied in different domains, in particular in classifying over images, for which the concept of convolution with a filter comes naturally. Unfortunately, the requirement of a distance (or, at least, of a neighbourhood function) in the input feature space has so far prevented its direct use on data types such as omics data. However, a number of omics data are metrizable, i.e., they can be endowed with a metric structure, enabling to adopt a convolutional based deep learning framework, e.g., for prediction. We propose a generalized solution for CNNs on omics data, implemented through a dedicated Keras layer. In particular, for metagenomics data, a metric can be derived from the patristic distance on the phylogenetic tree. For transcriptomics data, we combine Gene Ontology semantic similarity and gene co-expression to define a distance; the function is defined through a multilayer network where 3 layers are defined by the GO mutual semantic similarity while the fourth one by gene co-expression. As a general tool, feature distance on omics data is enabled by OmicsConv, a novel Keras layer, obtaining OmicsCNN, a dedicated deep learning framework. Here we demonstrate OmicsCNN on gut microbiota sequencing data, for Inflammatory Bowel Disease (IBD) 16S data, first on synthetic data and then a metagenomics collection of gut microbiota of 222 IBD patients.

Diffusion geometry unravels the emergence of functional clusters in collective phenomena

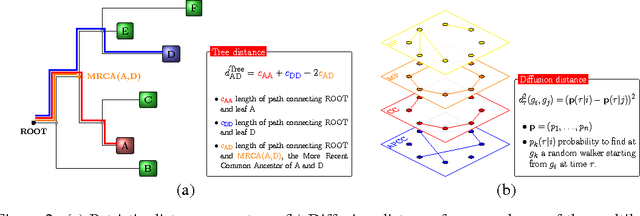
Collective phenomena emerge from the interaction of natural or artificial units with a complex organization. The interplay between structural patterns and dynamics might induce functional clusters that, in general, are different from topological ones. In biological systems, like the human brain, the overall functionality is often favored by the interplay between connectivity and synchronization dynamics, with functional clusters that do not coincide with anatomical modules in most cases. In social, socio-technical and engineering systems, the quest for consensus favors the emergence of clusters. Despite the unquestionable evidence for mesoscale organization of many complex systems and the heterogeneity of their inter-connectivity, a way to predict and identify the emergence of functional modules in collective phenomena continues to elude us. Here, we propose an approach based on random walk dynamics to define the diffusion distance between any pair of units in a networked system. Such a metric allows to exploit the underlying diffusion geometry to provide a unifying framework for the intimate relationship between metastable synchronization, consensus and random search dynamics in complex networks, pinpointing the functional mesoscale organization of synthetic and biological systems.