mGNN: Generalizing the Graph Neural Networks to the Multilayer Case

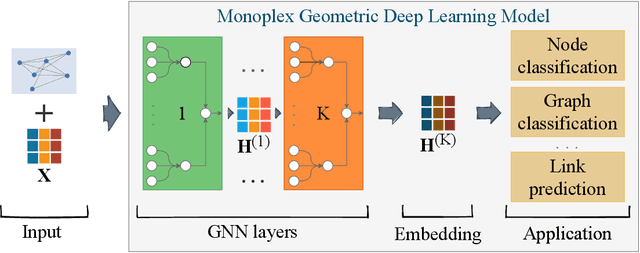
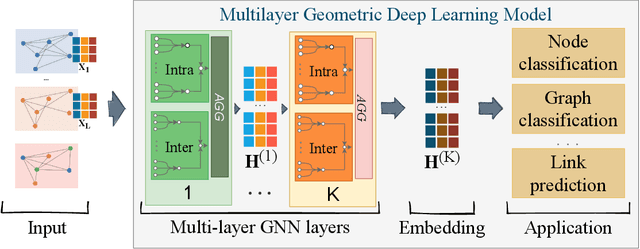
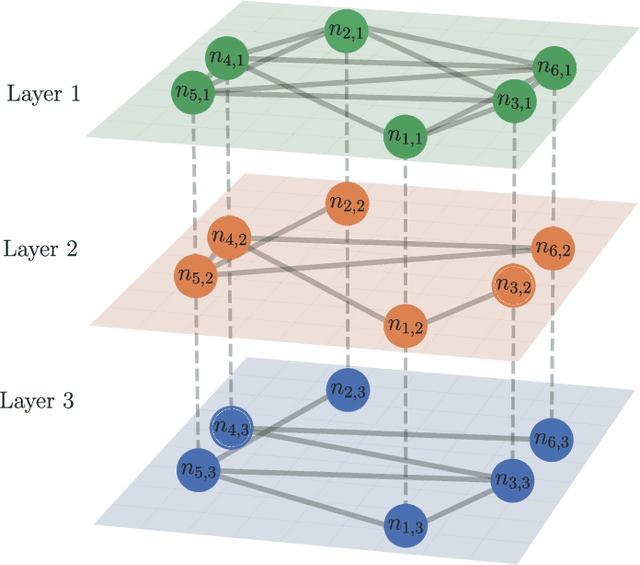
Networks are a powerful tool to model complex systems, and the definition of many Graph Neural Networks (GNN), Deep Learning algorithms that can handle networks, has opened a new way to approach many real-world problems that would be hardly or even untractable. In this paper, we propose mGNN, a framework meant to generalize GNNs to the case of multi-layer networks, i.e., networks that can model multiple kinds of interactions and relations between nodes. Our approach is general (i.e., not task specific) and has the advantage of extending any type of GNN without any computational overhead. We test the framework into three different tasks (node and network classification, link prediction) to validate it.

wsGAT: Weighted and Signed Graph Attention Networks for Link Prediction

Graph Neural Networks (GNNs) have been widely used to learn representations on graphs and tackle many real-world problems from a wide range of domains. In this paper we propose wsGAT, an extension of the Graph Attention Network (GAT) layers, meant to address the lack of GNNs that can handle graphs with signed and weighted links, which are ubiquitous, for instance, in trust and correlation networks. We first evaluate the performance of our proposal by comparing against GCNII in the weighed link prediction task, and against SGCN in the link sign prediction task. After that, we combine the two tasks and show their performance on predicting the signed weight of links, and their existence. Our results on real-world networks show that models with wsGAT layers outperform the ones with GCNII and SGCN layers, and that there is no loss in performance when signed weights are predicted.

Machine learning dismantling and early-warning signals of disintegration in complex systems

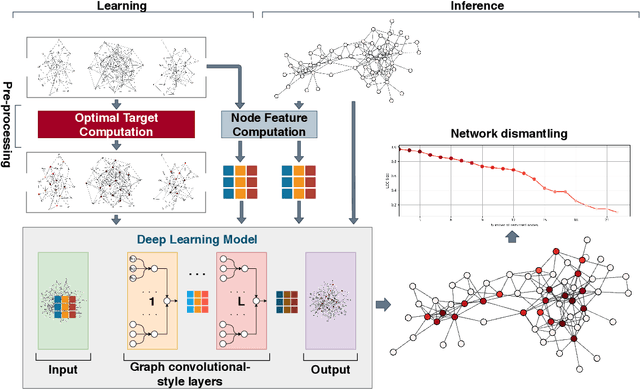
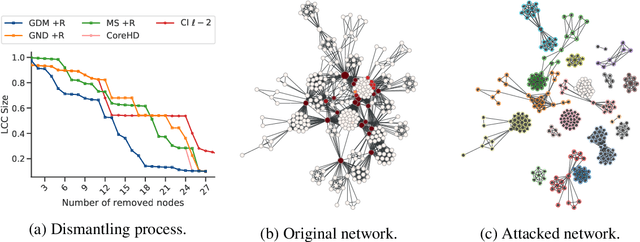
From physics to engineering, biology and social science, natural and artificial systems are characterized by interconnected topologies whose features - e.g., heterogeneous connectivity, mesoscale organization, hierarchy - affect their robustness to external perturbations, such as targeted attacks to their units. Identifying the minimal set of units to attack to disintegrate a complex network, i.e. network dismantling, is a computationally challenging (NP-hard) problem which is usually attacked with heuristics. Here, we show that a machine trained to dismantle relatively small systems is able to identify higher-order topological patterns, allowing to disintegrate large-scale social, infrastructural and technological networks more efficiently than human-based heuristics. Remarkably, the machine assesses the probability that next attacks will disintegrate the system, providing a quantitative method to quantify systemic risk and detect early-warning signals of system's collapse. This demonstrates that machine-assisted analysis can be effectively used for policy and decision making to better quantify the fragility of complex systems and their response to shocks.

Learning fine-grained search space pruning and heuristics for combinatorial optimization

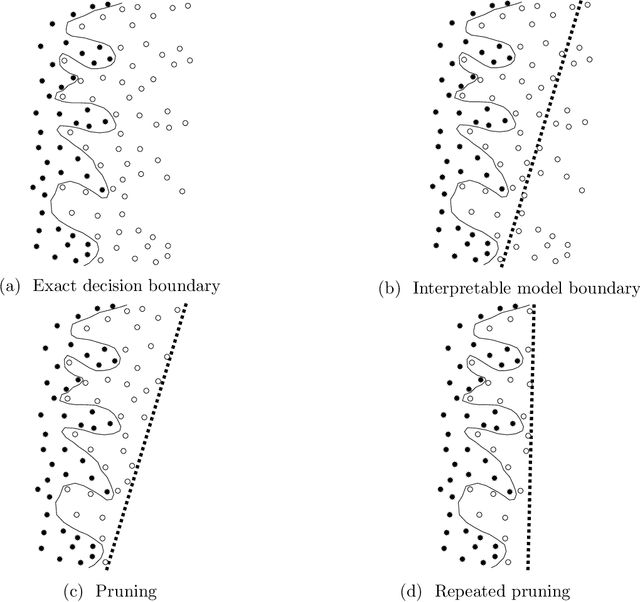
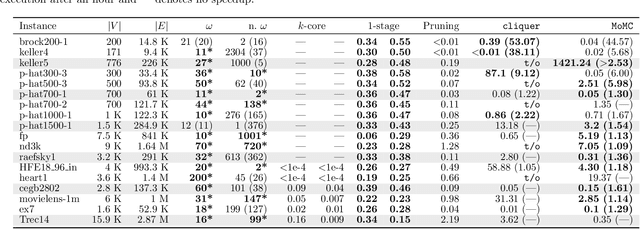
Combinatorial optimization problems arise in a wide range of applications from diverse domains. Many of these problems are NP-hard and designing efficient heuristics for them requires considerable time and experimentation. On the other hand, the number of optimization problems in the industry continues to grow. In recent years, machine learning techniques have been explored to address this gap. We propose a framework for leveraging machine learning techniques to scale-up exact combinatorial optimization algorithms. In contrast to the existing approaches based on deep-learning, reinforcement learning and restricted Boltzmann machines that attempt to directly learn the output of the optimization problem from its input (with limited success), our framework learns the relatively simpler task of pruning the elements in order to reduce the size of the problem instances. In addition, our framework uses only interpretable learning models based on intuitive features and thus the learning process provides deeper insights into the optimization problem and the instance class, that can be used for designing better heuristics. For the classical maximum clique enumeration problem, we show that our framework can prune a large fraction of the input graph (around 99 % of nodes in case of sparse graphs) and still detect almost all of the maximum cliques. This results in several fold speedups of state-of-the-art algorithms. Furthermore, the model used in our framework highlights that the chi-squared value of neighborhood degree has a statistically significant correlation with the presence of a node in a maximum clique, particularly in dense graphs which constitute a significant challenge for modern solvers. We leverage this insight to design a novel heuristic for this problem outperforming the state-of-the-art. Our heuristic is also of independent interest for maximum clique detection and enumeration.

Learning Multi-Stage Sparsification for Maximum Clique Enumeration

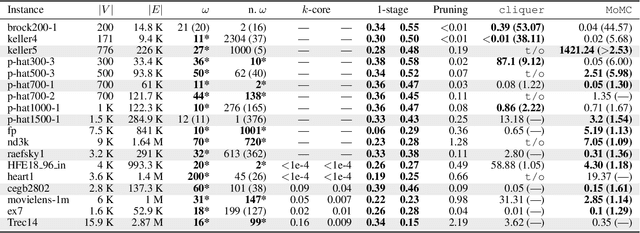
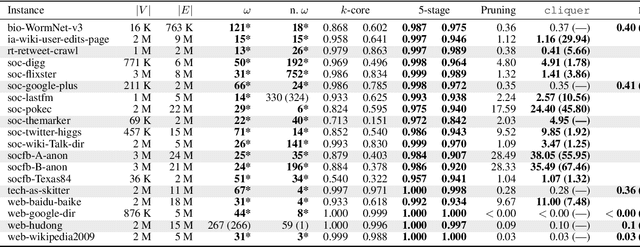
We propose a multi-stage learning approach for pruning the search space of maximum clique enumeration, a fundamental computationally difficult problem arising in various network analysis tasks. In each stage, our approach learns the characteristics of vertices in terms of various neighborhood features and leverage them to prune the set of vertices that are likely not contained in any maximum clique. Furthermore, we demonstrate that our approach is domain independent -- the same small set of features works well on graph instances from different domain. Compared to the state-of-the-art heuristics and preprocessing strategies, the advantages of our approach are that (i) it does not require any estimate on the maximum clique size at runtime and (ii) we demonstrate it to be effective also for dense graphs. In particular, for dense graphs, we typically prune around 30 \% of the vertices resulting in speedups of up to 53 times for state-of-the-art solvers while generally preserving the size of the maximum clique (though some maximum cliques may be lost). For large real-world sparse graphs, we routinely prune over 99 \% of the vertices resulting in several tenfold speedups at best, typically with no impact on solution quality.