Learning Multi-Stage Sparsification for Maximum Clique Enumeration
Paper and Code
Sep 12, 2019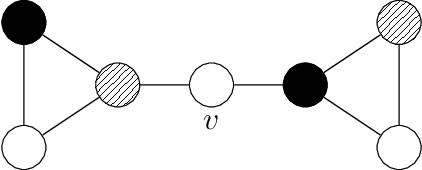

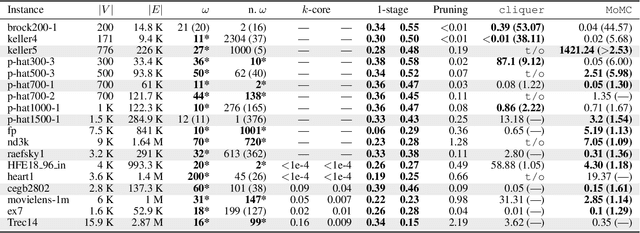
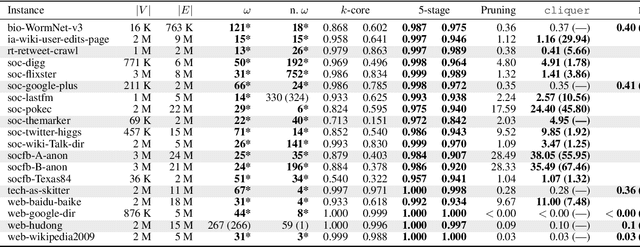
We propose a multi-stage learning approach for pruning the search space of maximum clique enumeration, a fundamental computationally difficult problem arising in various network analysis tasks. In each stage, our approach learns the characteristics of vertices in terms of various neighborhood features and leverage them to prune the set of vertices that are likely not contained in any maximum clique. Furthermore, we demonstrate that our approach is domain independent -- the same small set of features works well on graph instances from different domain. Compared to the state-of-the-art heuristics and preprocessing strategies, the advantages of our approach are that (i) it does not require any estimate on the maximum clique size at runtime and (ii) we demonstrate it to be effective also for dense graphs. In particular, for dense graphs, we typically prune around 30 \% of the vertices resulting in speedups of up to 53 times for state-of-the-art solvers while generally preserving the size of the maximum clique (though some maximum cliques may be lost). For large real-world sparse graphs, we routinely prune over 99 \% of the vertices resulting in several tenfold speedups at best, typically with no impact on solution quality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge