On the Impact of Random Node Sampling on Adaptive Diffusion Networks

In this paper, we analyze the effects of random sampling on adaptive diffusion networks. These networks consist in a collection of nodes that can measure and process data, and that can communicate with each other to pursue a common goal of estimating an unknown system. In particular, we consider in our theoretical analysis the diffusion least-mean-squares algorithm in a scenario in which the nodes are randomly sampled. Hence, each node may or may not adapt its local estimate at a certain iteration. Our model shows that, if the nodes cooperate, a reduction in the sampling probability leads to a slight decrease in the steady-state Network Mean-Square Deviation (NMSD), assuming that the environment is stationary and that all other parameters of the algorithm are kept fixed. Furthermore, under certain circumstances, this can also ensure the stability of the algorithm in situations in which it would otherwise be unstable. Although counter-intuitive, our findings are backed by simulation results, which match the theoretical curves well.

Chaotic properties of an FIR filtered Hénon map

When chaotic signals are used in practical communication systems, it is essential to control and eventually limit the spectral bandwidth occupied by these signals. One way to achieve this goal is to insert a discrete-time filter into a nonlinear map that generates chaotic signals. However, this can completely change the dynamic properties of the original map. Considering this situation, this paper presents a series of numerical experiments aimed at obtaining the Lyapunov exponents of the signals generated by the two-dimensional H\'enon map with a set of prototypical finite impulse response (FIR) filters added in the feedback loop. Our results show that the number of filter coefficients and the location of the zeros have a significant and complex impact on the behavior of the generated signals. Therefore, FIR filters should be carefully designed to preserve or suppress chaos in practical applications.

Combinations of Adaptive Filters

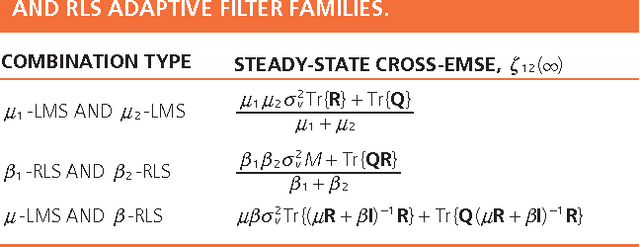
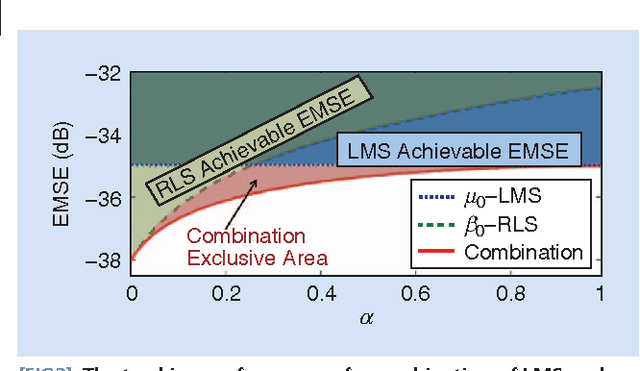
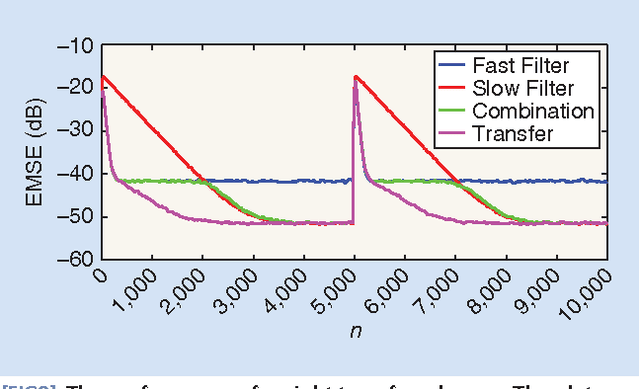
Adaptive filters are at the core of many signal processing applications, ranging from acoustic noise supression to echo cancelation, array beamforming, channel equalization, to more recent sensor network applications in surveillance, target localization, and tracking. A trending approach in this direction is to recur to in-network distributed processing in which individual nodes implement adaptation rules and diffuse their estimation to the network. When the a priori knowledge about the filtering scenario is limited or imprecise, selecting the most adequate filter structure and adjusting its parameters becomes a challenging task, and erroneous choices can lead to inadequate performance. To address this difficulty, one useful approach is to rely on combinations of adaptive structures. The combination of adaptive filters exploits to some extent the same divide and conquer principle that has also been successfully exploited by the machine-learning community (e.g., in bagging or boosting). In particular, the problem of combining the outputs of several learning algorithms (mixture of experts) has been studied in the computational learning field under a different perspective: rather than studying the expected performance of the mixture, deterministic bounds are derived that apply to individual sequences and, therefore, reflect worst-case scenarios. These bounds require assumptions different from the ones typically used in adaptive filtering, which is the emphasis of this overview article. We review the key ideas and principles behind these combination schemes, with emphasis on design rules. We also illustrate their performance with a variety of examples.

Adaptive Diffusion Schemes for Heterogeneous Networks

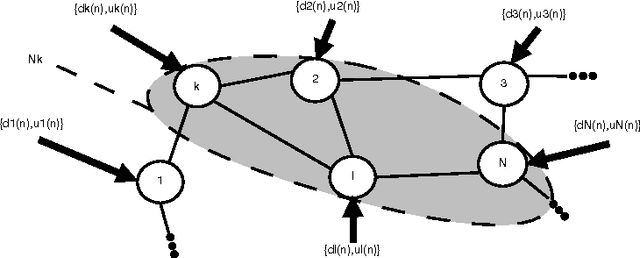
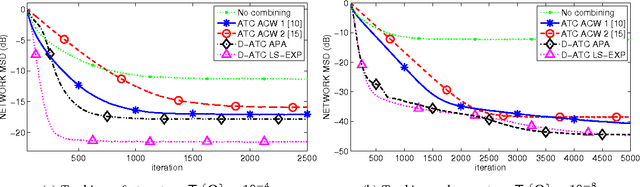
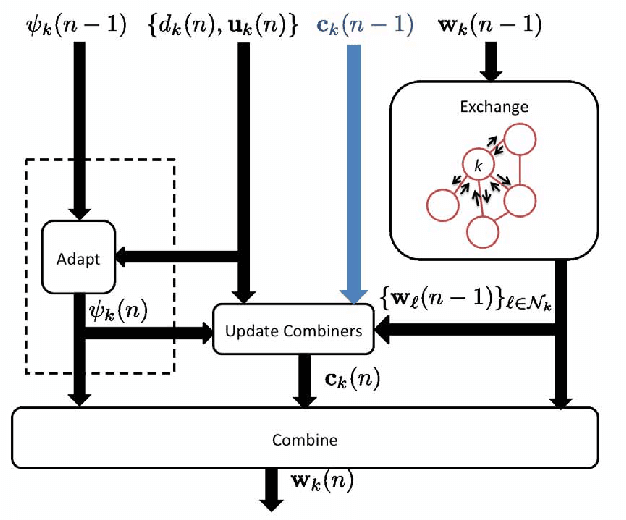
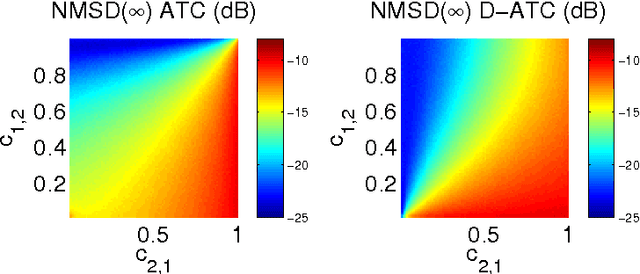
In this paper, we deal with distributed estimation problems in diffusion networks with heterogeneous nodes, i.e., nodes that either implement different adaptive rules or differ in some other aspect such as the filter structure or length, or step size. Although such heterogeneous networks have been considered from the first works on diffusion networks, obtaining practical and robust schemes to adaptively adjust the combiners in different scenarios is still an open problem. In this paper, we study a diffusion strategy specially designed and suited to heterogeneous networks. Our approach is based on two key ingredients: 1) the adaptation and combination phases are completely decoupled, so that network nodes keep purely local estimations at all times; and 2) combiners are adapted to minimize estimates of the network mean-square-error. Our scheme is compared with the standard Adapt-then-Combine scheme and theoretically analyzed using energy conservation arguments. Several experiments involving networks with heterogeneous nodes show that the proposed decoupled Adapt-then-Combine approach with adaptive combiners outperforms other state-of-the-art techniques, becoming a competitive approach in these scenarios.