Vitor H. Nascimento
Combinations of Adaptive Filters
Dec 22, 2021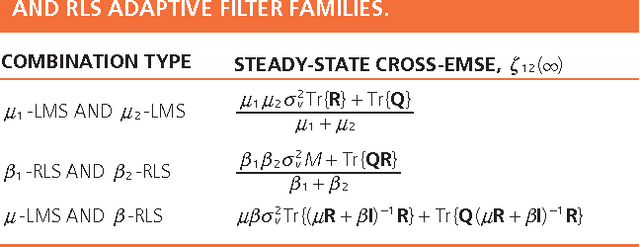

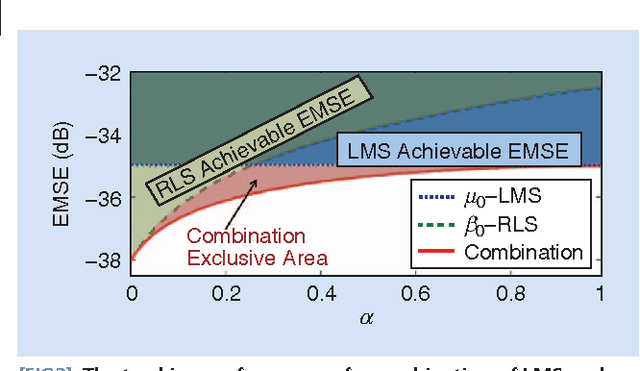
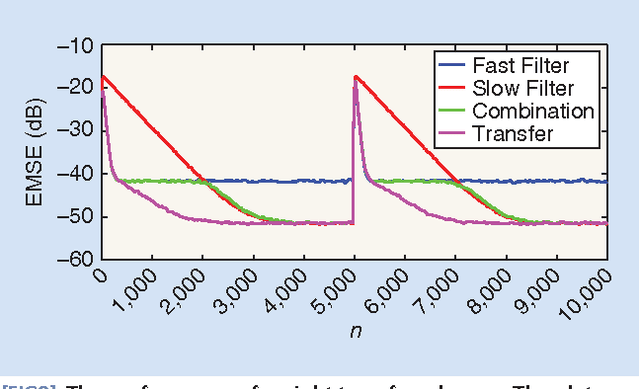
Abstract:Adaptive filters are at the core of many signal processing applications, ranging from acoustic noise supression to echo cancelation, array beamforming, channel equalization, to more recent sensor network applications in surveillance, target localization, and tracking. A trending approach in this direction is to recur to in-network distributed processing in which individual nodes implement adaptation rules and diffuse their estimation to the network. When the a priori knowledge about the filtering scenario is limited or imprecise, selecting the most adequate filter structure and adjusting its parameters becomes a challenging task, and erroneous choices can lead to inadequate performance. To address this difficulty, one useful approach is to rely on combinations of adaptive structures. The combination of adaptive filters exploits to some extent the same divide and conquer principle that has also been successfully exploited by the machine-learning community (e.g., in bagging or boosting). In particular, the problem of combining the outputs of several learning algorithms (mixture of experts) has been studied in the computational learning field under a different perspective: rather than studying the expected performance of the mixture, deterministic bounds are derived that apply to individual sequences and, therefore, reflect worst-case scenarios. These bounds require assumptions different from the ones typically used in adaptive filtering, which is the emphasis of this overview article. We review the key ideas and principles behind these combination schemes, with emphasis on design rules. We also illustrate their performance with a variety of examples.
Study of Robust Adaptive Beamforming Based on Low-Complexity DFT Spatial Sampling
Jun 23, 2021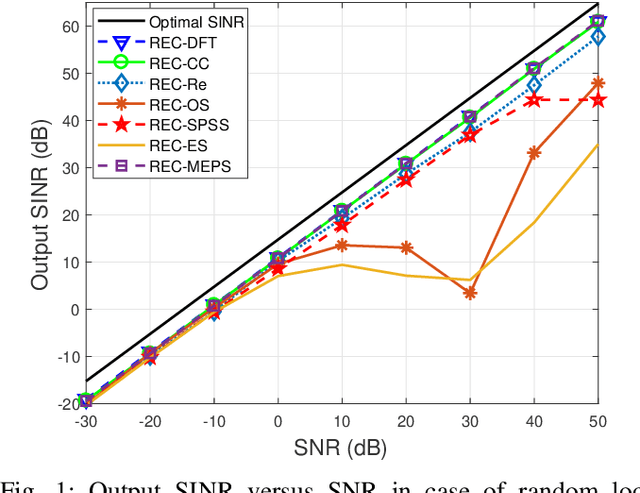


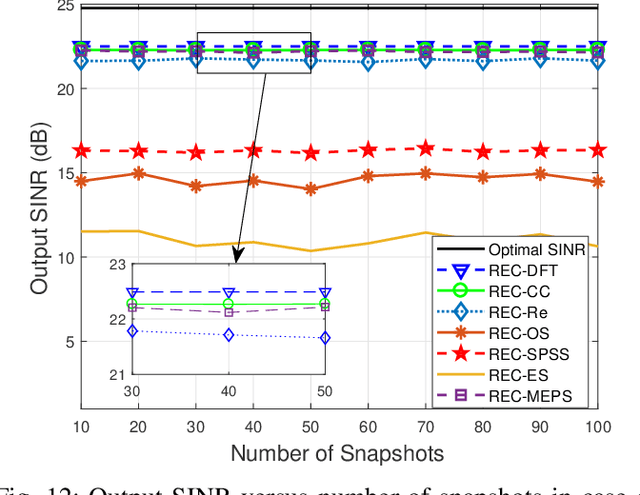
Abstract:In this paper, a novel and robust algorithm is proposed for adaptive beamforming based on the idea of reconstructing the autocorrelation sequence (ACS) of a random process from a set of measured data. This is obtained from the first column and the first row of the sample covariance matrix (SCM) after averaging along its diagonals. Then, the power spectrum of the correlation sequence is estimated using the discrete Fourier transform (DFT). The DFT coefficients corresponding to the angles within the noise-plus-interference region are used to reconstruct the noise-plus-interference covariance matrix (NPICM), while the desired signal covariance matrix (DSCM) is estimated by identifying and removing the noise-plus-interference component from the SCM. In particular, the spatial power spectrum of the estimated received signal is utilized to compute the correlation sequence corresponding to the noise-plus-interference in which the dominant DFT coefficient of the noise-plus-interference is captured. A key advantage of the proposed adaptive beamforming is that only little prior information is required. Specifically, an imprecise knowledge of the array geometry and of the angular sectors in which the interferences are located is needed. Simulation results demonstrate that compared with previous reconstruction-based beamformers, the proposed approach can achieve better overall performance in the case of multiple mismatches over a very large range of input signal-to-noise ratios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge