Osman Kukrer
Study of Robust Adaptive Beamforming Based on Low-Complexity DFT Spatial Sampling
Jun 23, 2021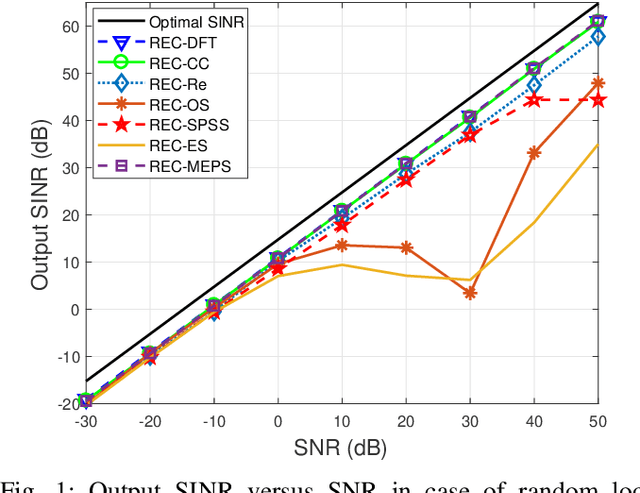


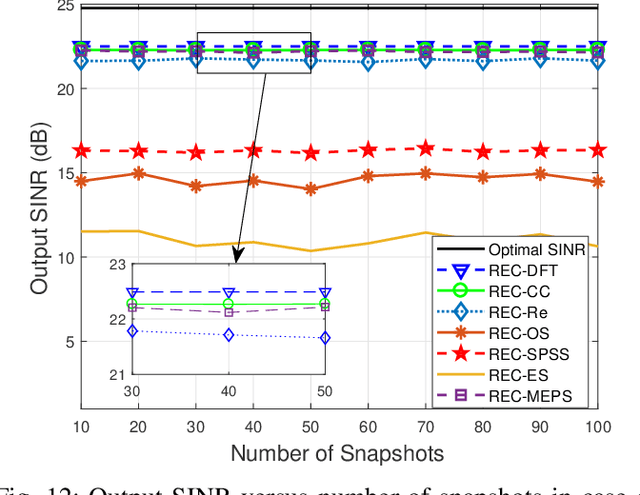
Abstract:In this paper, a novel and robust algorithm is proposed for adaptive beamforming based on the idea of reconstructing the autocorrelation sequence (ACS) of a random process from a set of measured data. This is obtained from the first column and the first row of the sample covariance matrix (SCM) after averaging along its diagonals. Then, the power spectrum of the correlation sequence is estimated using the discrete Fourier transform (DFT). The DFT coefficients corresponding to the angles within the noise-plus-interference region are used to reconstruct the noise-plus-interference covariance matrix (NPICM), while the desired signal covariance matrix (DSCM) is estimated by identifying and removing the noise-plus-interference component from the SCM. In particular, the spatial power spectrum of the estimated received signal is utilized to compute the correlation sequence corresponding to the noise-plus-interference in which the dominant DFT coefficient of the noise-plus-interference is captured. A key advantage of the proposed adaptive beamforming is that only little prior information is required. Specifically, an imprecise knowledge of the array geometry and of the angular sectors in which the interferences are located is needed. Simulation results demonstrate that compared with previous reconstruction-based beamformers, the proposed approach can achieve better overall performance in the case of multiple mismatches over a very large range of input signal-to-noise ratios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge