Adaptive Diffusion Schemes for Heterogeneous Networks
Paper and Code
Aug 17, 2017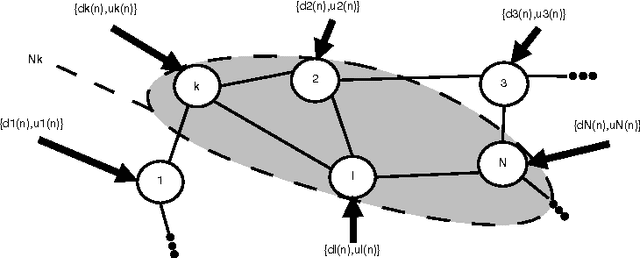
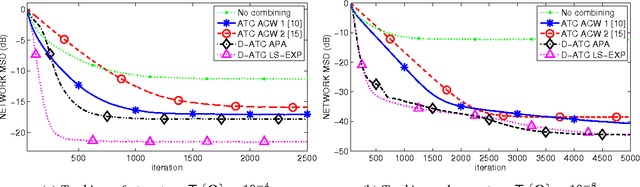
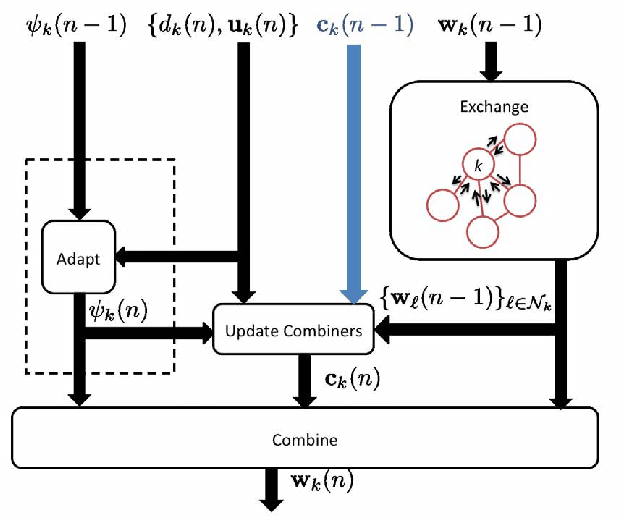
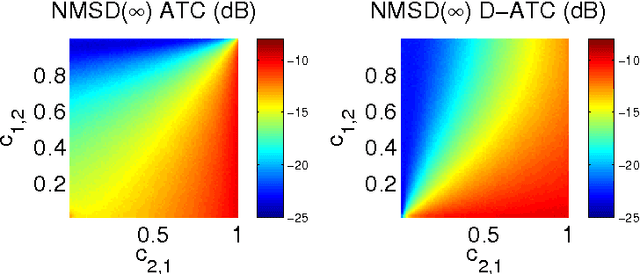
In this paper, we deal with distributed estimation problems in diffusion networks with heterogeneous nodes, i.e., nodes that either implement different adaptive rules or differ in some other aspect such as the filter structure or length, or step size. Although such heterogeneous networks have been considered from the first works on diffusion networks, obtaining practical and robust schemes to adaptively adjust the combiners in different scenarios is still an open problem. In this paper, we study a diffusion strategy specially designed and suited to heterogeneous networks. Our approach is based on two key ingredients: 1) the adaptation and combination phases are completely decoupled, so that network nodes keep purely local estimations at all times; and 2) combiners are adapted to minimize estimates of the network mean-square-error. Our scheme is compared with the standard Adapt-then-Combine scheme and theoretically analyzed using energy conservation arguments. Several experiments involving networks with heterogeneous nodes show that the proposed decoupled Adapt-then-Combine approach with adaptive combiners outperforms other state-of-the-art techniques, becoming a competitive approach in these scenarios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge