Chaotic properties of an FIR filtered Hénon map

When chaotic signals are used in practical communication systems, it is essential to control and eventually limit the spectral bandwidth occupied by these signals. One way to achieve this goal is to insert a discrete-time filter into a nonlinear map that generates chaotic signals. However, this can completely change the dynamic properties of the original map. Considering this situation, this paper presents a series of numerical experiments aimed at obtaining the Lyapunov exponents of the signals generated by the two-dimensional H\'enon map with a set of prototypical finite impulse response (FIR) filters added in the feedback loop. Our results show that the number of filter coefficients and the location of the zeros have a significant and complex impact on the behavior of the generated signals. Therefore, FIR filters should be carefully designed to preserve or suppress chaos in practical applications.

A filtered Hénon map

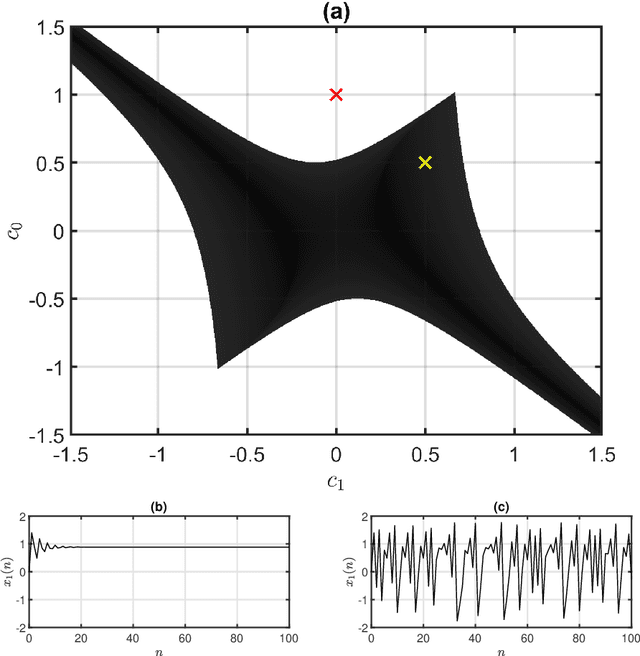
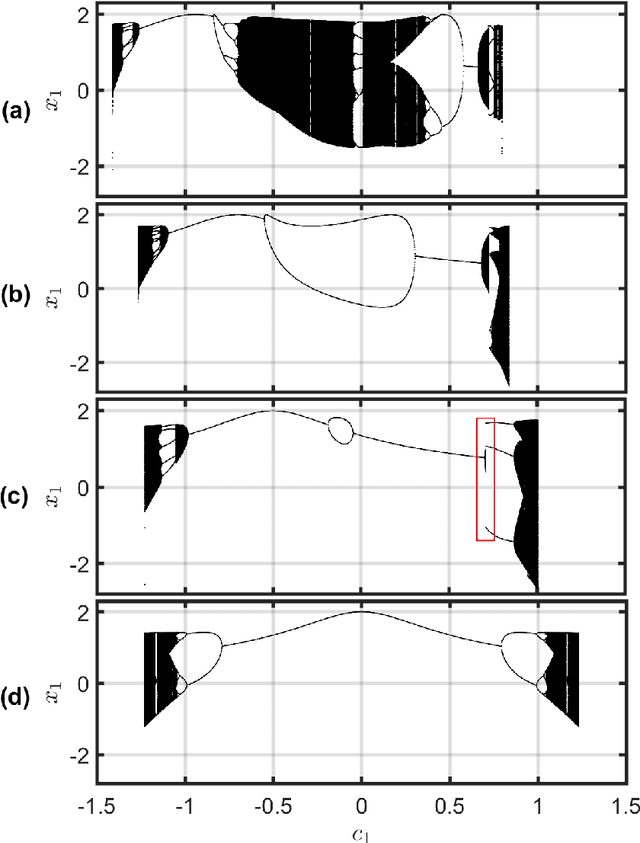
In this paper, we use Lyapunov exponents to analyze how the dynamical properties of the H\'enon map change as a function of the coefficients of a linear filter inserted in its feedback loop. We show that the generated orbits can be chaotic or not, depending on the filter coefficients. The dynamics of the system presents complex behavior, including cascades of bifurcations, coexistence of attractors, crises, and "shrimps". The obtained results are relevant in the context of bandlimited chaos-based communication systems, that have recently been proposed in the literature.