Information Leakage Games: Exploring Information as a Utility Function

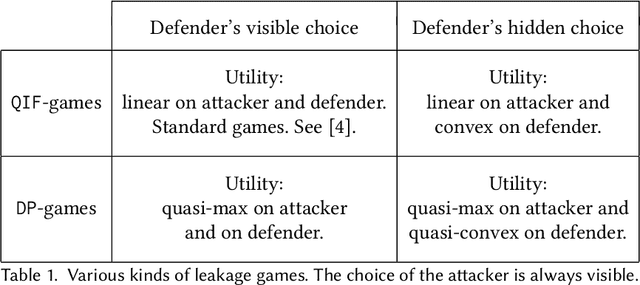
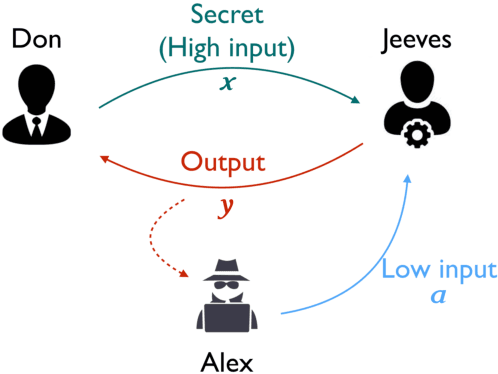
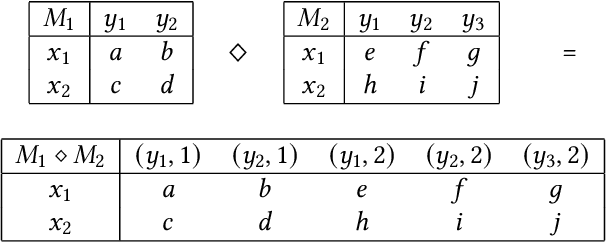
A common goal in the areas of secure information flow and privacy is to build effective defenses against unwanted leakage of information. To this end, one must be able to reason about potential attacks and their interplay with possible defenses. In this paper we propose a game-theoretic framework to formalize strategies of attacker and defender in the context of information leakage, and provide a basis for developing optimal defense methods. A crucial novelty of our games is that their utility is given by information leakage, which in some cases may behave in a non-linear way. This causes a significant deviation from classic game theory, in which utility functions are linear with respect to players' strategies. Hence, a key contribution of this paper is the establishment of the foundations of information leakage games. We consider two main categories of games, depending on the particular notion of information leakage being captured. The first category, which we call QIF-games, is tailored for the theory of quantitative information flow (QIF). The second one, which we call DP-games, corresponds to differential privacy (DP).

BrazilDAM: A Benchmark dataset for Tailings Dam Detection

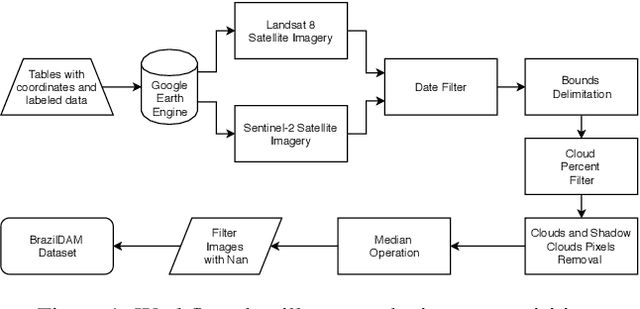
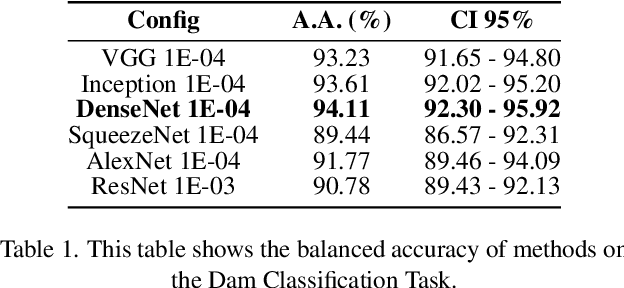
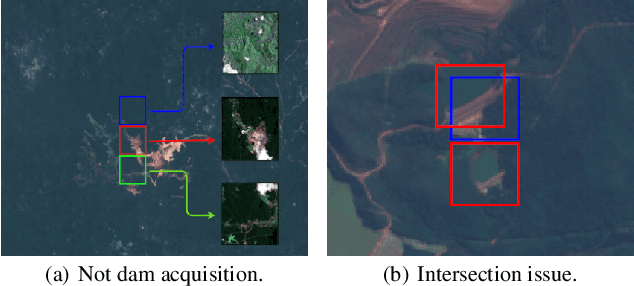
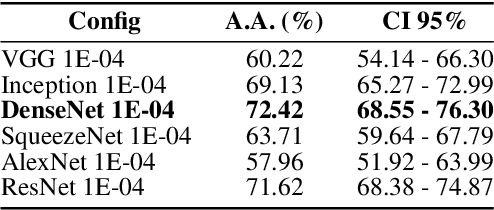
In this work we present BrazilDAM, a novel public dataset based on Sentinel-2 and Landsat-8 satellite images covering all tailings dams cataloged by the Brazilian National Mining Agency (ANM). The dataset was built using georeferenced images from 769 dams, recorded between 2016 and 2019. The time series were processed in order to produce cloud free images. The dams contain mining waste from different ore categories and have highly varying shapes, areas and volumes, making BrazilDAM particularly interesting and challenging to be used in machine learning benchmarks. The original catalog contains, besides the dam coordinates, information about: the main ore, constructive method, risk category, and associated potential damage. To evaluate BrazilDAM's predictive potential we performed classification essays using state-of-the-art deep Convolutional Neural Network (CNNs). In the experiments, we achieved an average classification accuracy of 94.11\% in tailing dam binary classification task. In addition, others four setups of experiments were made using the complementary information from the original catalog, exhaustively exploiting the capacity of the proposed dataset.

A Comparative Study on Unsupervised Domain Adaptation Approaches for Coffee Crop Mapping

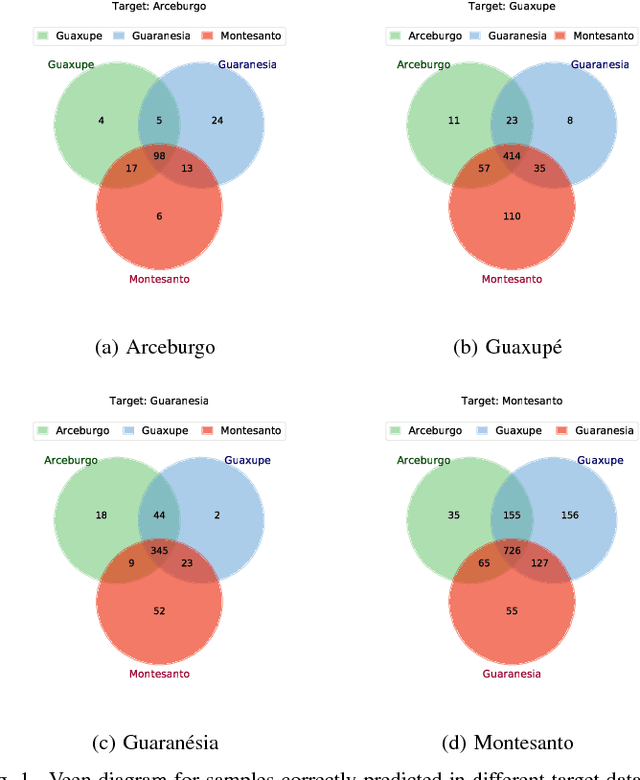
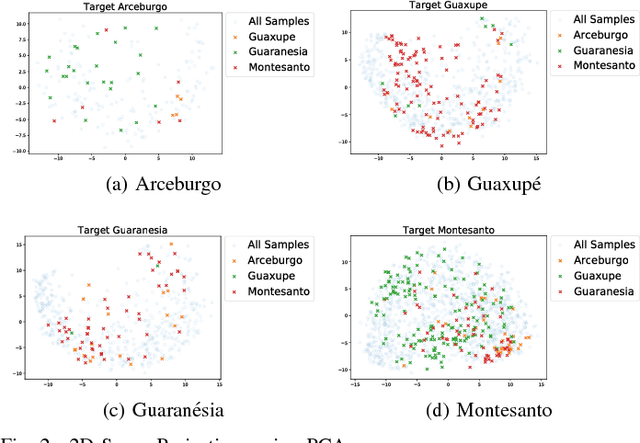
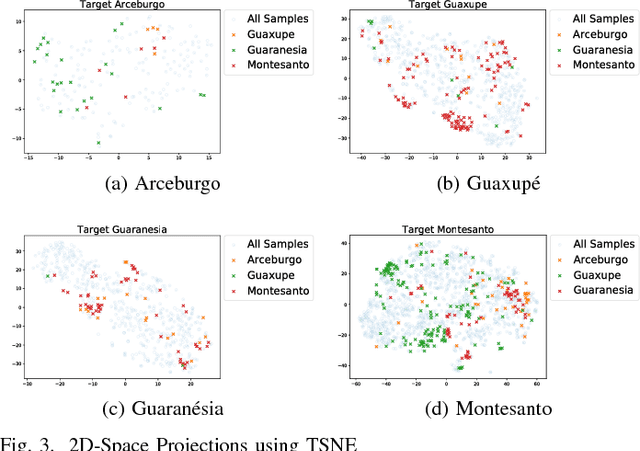
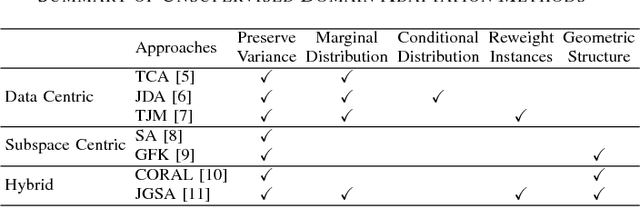
In this work, we investigate the application of existing unsupervised domain adaptation (UDA) approaches to the task of transferring knowledge between crop regions having different coffee patterns. Given a geographical region with fully mapped coffee plantations, we observe that this knowledge can be used to train a classifier and to map a new county with no need of samples indicated in the target region. Experimental results show that transferring knowledge via some UDA strategies performs better than just applying a classifier trained in a region to predict coffee crops in a new one. However, UDA methods may lead to negative transfer, which may indicate that domains are too different that transferring knowledge is not appropriate. We also verify that normalization affect significantly some UDA methods; we observe a meaningful complementary contribution between coffee crops data; and a visual behavior suggests an existent of a cluster of samples that are more likely to be drawn from a specific data.

Computational Aspects of the Calculus of Structure

Logic is the science of correct inferences and a logical system is a tool to prove assertions in a certain logic in a correct way. There are many logical systems, and many ways of formalizing them, e.g., using natural deduction or sequent calculus. Calculus of structures (CoS) is a new formalism proposed by Alessio Guglielmi in 2004 that generalizes sequent calculus in the sense that inference rules can be applied at any depth inside a formula, rather than only to the main connective. With this feature, proofs in CoS are shorter than in any other formalism supporting analytical proofs. Although it is great to have the freedom and expressiveness of CoS, under the point of view of proof search more freedom means a larger search space. And that should be restricted when looking for complete automation of deductive systems. Some efforts were made to reduce this non-determinism, but they are all basically operational approaches, and no solid theoretical result regarding the computational behaviour of CoS has been achieved so far. The main focus of this thesis is to discuss ways to propose a proof search strategy for CoS suitable to implementation. This strategy should be theoretical instead of purely operational. We introduce the concept of incoherence number of substructures inside structures and we use this concept to achieve our main result: there is an algorithm that, according to our conjecture, corresponds to a proof search strategy to every provable structure in the subsystem of FBV (the multiplicative linear logic MLL plus the rule mix) containing only pairwise distinct atoms. Our algorithm is implemented and we believe our strategy is a good starting point to exploit the computational aspects of CoS in more general systems, like BV itself.