Information Leakage Games: Exploring Information as a Utility Function
Paper and Code
Dec 22, 2020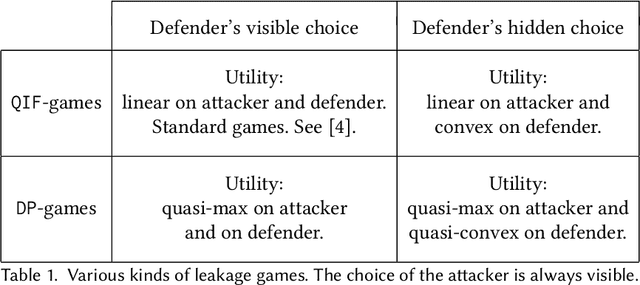
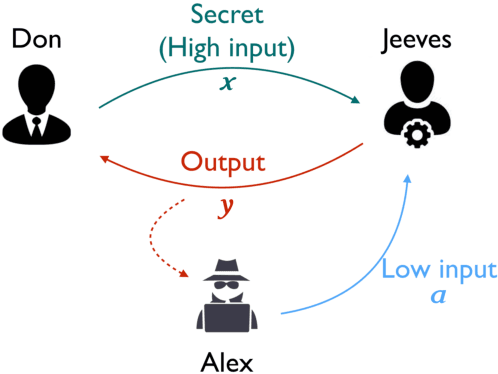

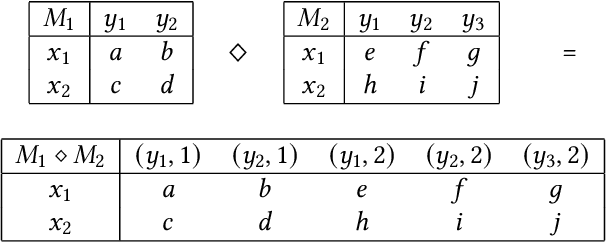
A common goal in the areas of secure information flow and privacy is to build effective defenses against unwanted leakage of information. To this end, one must be able to reason about potential attacks and their interplay with possible defenses. In this paper we propose a game-theoretic framework to formalize strategies of attacker and defender in the context of information leakage, and provide a basis for developing optimal defense methods. A crucial novelty of our games is that their utility is given by information leakage, which in some cases may behave in a non-linear way. This causes a significant deviation from classic game theory, in which utility functions are linear with respect to players' strategies. Hence, a key contribution of this paper is the establishment of the foundations of information leakage games. We consider two main categories of games, depending on the particular notion of information leakage being captured. The first category, which we call QIF-games, is tailored for the theory of quantitative information flow (QIF). The second one, which we call DP-games, corresponds to differential privacy (DP).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge