PhysAug: A Physical-guided and Frequency-based Data Augmentation for Single-Domain Generalized Object Detection

Single-Domain Generalized Object Detection~(S-DGOD) aims to train on a single source domain for robust performance across a variety of unseen target domains by taking advantage of an object detector. Existing S-DGOD approaches often rely on data augmentation strategies, including a composition of visual transformations, to enhance the detector's generalization ability. However, the absence of real-world prior knowledge hinders data augmentation from contributing to the diversity of training data distributions. To address this issue, we propose PhysAug, a novel physical model-based non-ideal imaging condition data augmentation method, to enhance the adaptability of the S-DGOD tasks. Drawing upon the principles of atmospheric optics, we develop a universal perturbation model that serves as the foundation for our proposed PhysAug. Given that visual perturbations typically arise from the interaction of light with atmospheric particles, the image frequency spectrum is harnessed to simulate real-world variations during training. This approach fosters the detector to learn domain-invariant representations, thereby enhancing its ability to generalize across various settings. Without altering the network architecture or loss function, our approach significantly outperforms the state-of-the-art across various S-DGOD datasets. In particular, it achieves a substantial improvement of $7.3\%$ and $7.2\%$ over the baseline on DWD and Cityscape-C, highlighting its enhanced generalizability in real-world settings.

Object Gaussian for Monocular 6D Pose Estimation from Sparse Views

Monocular object pose estimation, as a pivotal task in computer vision and robotics, heavily depends on accurate 2D-3D correspondences, which often demand costly CAD models that may not be readily available. Object 3D reconstruction methods offer an alternative, among which recent advancements in 3D Gaussian Splatting (3DGS) afford a compelling potential. Yet its performance still suffers and tends to overfit with fewer input views. Embracing this challenge, we introduce SGPose, a novel framework for sparse view object pose estimation using Gaussian-based methods. Given as few as ten views, SGPose generates a geometric-aware representation by starting with a random cuboid initialization, eschewing reliance on Structure-from-Motion (SfM) pipeline-derived geometry as required by traditional 3DGS methods. SGPose removes the dependence on CAD models by regressing dense 2D-3D correspondences between images and the reconstructed model from sparse input and random initialization, while the geometric-consistent depth supervision and online synthetic view warping are key to the success. Experiments on typical benchmarks, especially on the Occlusion LM-O dataset, demonstrate that SGPose outperforms existing methods even under sparse view constraints, under-scoring its potential in real-world applications.

PU-EVA: An Edge Vector based Approximation Solution for Flexible-scale Point Cloud Upsampling

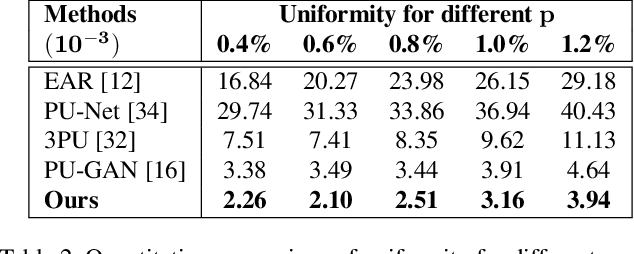
High-quality point clouds have practical significance for point-based rendering, semantic understanding, and surface reconstruction. Upsampling sparse, noisy and nonuniform point clouds for a denser and more regular approximation of target objects is a desirable but challenging task. Most existing methods duplicate point features for upsampling, constraining the upsampling scales at a fixed rate. In this work, the flexible upsampling rates are achieved via edge vector based affine combinations, and a novel design of Edge Vector based Approximation for Flexible-scale Point clouds Upsampling (PU-EVA) is proposed. The edge vector based approximation encodes the neighboring connectivity via affine combinations based on edge vectors, and restricts the approximation error within the second-order term of Taylor's Expansion. The EVA upsampling decouples the upsampling scales with network architecture, achieving the flexible upsampling rates in one-time training. Qualitative and quantitative evaluations demonstrate that the proposed PU-EVA outperforms the state-of-the-art in terms of proximity-to-surface, distribution uniformity, and geometric details preservation.