Path Signatures for Diversity in Probabilistic Trajectory Optimisation

Motion planning can be cast as a trajectory optimisation problem where a cost is minimised as a function of the trajectory being generated. In complex environments with several obstacles and complicated geometry, this optimisation problem is usually difficult to solve and prone to local minima. However, recent advancements in computing hardware allow for parallel trajectory optimisation where multiple solutions are obtained simultaneously, each initialised from a different starting point. Unfortunately, without a strategy preventing two solutions to collapse on each other, naive parallel optimisation can suffer from mode collapse diminishing the efficiency of the approach and the likelihood of finding a global solution. In this paper we leverage on recent advances in the theory of rough paths to devise an algorithm for parallel trajectory optimisation that promotes diversity over the range of solutions, therefore avoiding mode collapses and achieving better global properties. Our approach builds on path signatures and Hilbert space representations of trajectories, and connects parallel variational inference for trajectory estimation with diversity promoting kernels. We empirically demonstrate that this strategy achieves lower average costs than competing alternatives on a range of problems, from 2D navigation to robotic manipulators operating in cluttered environments.

Dual Online Stein Variational Inference for Control and Dynamics

Model predictive control (MPC) schemes have a proven track record for delivering aggressive and robust performance in many challenging control tasks, coping with nonlinear system dynamics, constraints, and observational noise. Despite their success, these methods often rely on simple control distributions, which can limit their performance in highly uncertain and complex environments. MPC frameworks must be able to accommodate changing distributions over system parameters, based on the most recent measurements. In this paper, we devise an implicit variational inference algorithm able to estimate distributions over model parameters and control inputs on-the-fly. The method incorporates Stein Variational gradient descent to approximate the target distributions as a collection of particles, and performs updates based on a Bayesian formulation. This enables the approximation of complex multi-modal posterior distributions, typically occurring in challenging and realistic robot navigation tasks. We demonstrate our approach on both simulated and real-world experiments requiring real-time execution in the face of dynamically changing environments.

DISCO: Double Likelihood-free Inference Stochastic Control

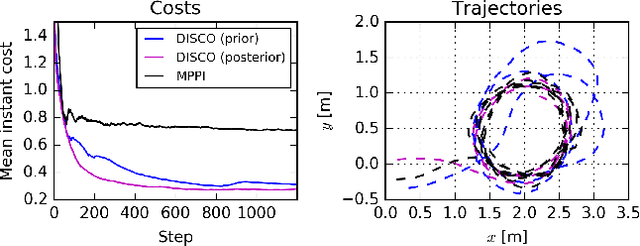
Accurate simulation of complex physical systems enables the development, testing, and certification of control strategies before they are deployed into the real systems. As simulators become more advanced, the analytical tractability of the differential equations and associated numerical solvers incorporated in the simulations diminishes, making them difficult to analyse. A potential solution is the use of probabilistic inference to assess the uncertainty of the simulation parameters given real observations of the system. Unfortunately the likelihood function required for inference is generally expensive to compute or totally intractable. In this paper we propose to leverage the power of modern simulators and recent techniques in Bayesian statistics for likelihood-free inference to design a control framework that is efficient and robust with respect to the uncertainty over simulation parameters. The posterior distribution over simulation parameters is propagated through a potentially non-analytical model of the system with the unscented transform, and a variant of the information theoretical model predictive control. This approach provides a more efficient way to evaluate trajectory roll outs than Monte Carlo sampling, reducing the online computation burden. Experiments show that the controller proposed attained superior performance and robustness on classical control and robotics tasks when compared to models not accounting for the uncertainty over model parameters.