Learning dynamical systems with biochemically informed neural ordinary differential equations

Ordinary differential equation models of biochemical reactions are often formulated as stoichiometric systems in which the dynamics arise from a collection of interacting processes. A central challenge is that the functional form of each process is rarely known a priori and may be difficult to infer from data. We propose biochemically informed neural ordinary differential equations (BINODEs), a neural-ODE framework that retains the stoichiometric structure of mechanistic models while representing individual processes by neural networks. In BINODEs, the outputs of neural network processes (NNPs) are mapped to state derivatives through a linear layer analogous to a stoichiometric matrix. This architecture allows biological side information, such as process-specific inputs, sign constraints, and monotonicity assumptions, to be built directly into the model. We characterize the approximation properties of NNPs for several standard biochemical rate laws and show that the proposed framework recovers both trajectories and process-level structure in Monod, Lotka--Volterra, pharmacokinetic, and ultradian endocrine models. These results suggest that BINODEs offer a useful compromise between mechanistic interpretability and data-driven flexibility for modeling partially known biochemical or biological dynamical systems.

Control of Medical Digital Twins with Artificial Neural Networks

The objective of personalized medicine is to tailor interventions to an individual patient's unique characteristics. A key technology for this purpose involves medical digital twins, computational models of human biology that can be personalized and dynamically updated to incorporate patient-specific data collected over time. Certain aspects of human biology, such as the immune system, are not easily captured with physics-based models, such as differential equations. Instead, they are often multi-scale, stochastic, and hybrid. This poses a challenge to existing model-based control and optimization approaches that cannot be readily applied to such models. Recent advances in automatic differentiation and neural-network control methods hold promise in addressing complex control problems. However, the application of these approaches to biomedical systems is still in its early stages. This work introduces dynamics-informed neural-network controllers as an alternative approach to control of medical digital twins. As a first use case for this method, the focus is on agent-based models, a versatile and increasingly common modeling platform in biomedicine. The effectiveness of the proposed neural-network control method is illustrated and benchmarked against other methods with two widely-used agent-based model types. The relevance of the method introduced here extends beyond medical digital twins to other complex dynamical systems.

Gradient-free training of neural ODEs for system identification and control using ensemble Kalman inversion

Ensemble Kalman inversion (EKI) is a sequential Monte Carlo method used to solve inverse problems within a Bayesian framework. Unlike backpropagation, EKI is a gradient-free optimization method that only necessitates the evaluation of artificial neural networks in forward passes. In this study, we examine the effectiveness of EKI in training neural ordinary differential equations (neural ODEs) for system identification and control tasks. To apply EKI to optimal control problems, we formulate inverse problems that incorporate a Tikhonov-type regularization term. Our numerical results demonstrate that EKI is an efficient method for training neural ODEs in system identification and optimal control problems, with runtime and quality of solutions that are competitive with commonly used gradient-based optimizers.

Visualizing high-dimensional loss landscapes with Hessian directions

Analyzing geometric properties of high-dimensional loss functions, such as local curvature and the existence of other optima around a certain point in loss space, can help provide a better understanding of the interplay between neural network structure, implementation attributes, and learning performance. In this work, we combine concepts from high-dimensional probability and differential geometry to study how curvature properties in lower-dimensional loss representations depend on those in the original loss space. We show that saddle points in the original space are rarely correctly identified as such in lower-dimensional representations if random projections are used. In such projections, the expected curvature in a lower-dimensional representation is proportional to the mean curvature in the original loss space. Hence, the mean curvature in the original loss space determines if saddle points appear, on average, as either minima, maxima, or almost flat regions. We use the connection between expected curvature and mean curvature (i.e., the normalized Hessian trace) to estimate the trace of Hessians without calculating the Hessian or Hessian-vector products as in Hutchinson's method. Because random projections are not able to correctly identify saddle information, we propose to study projections along Hessian directions that are associated with the largest and smallest principal curvatures. We connect our findings to the ongoing debate on loss landscape flatness and generalizability. Finally, we illustrate our method in numerical experiments on different image classifiers with up to about $7\times 10^6$ parameters.

Near-optimal control of dynamical systems with neural ordinary differential equations

Optimal control problems naturally arise in many scientific applications where one wishes to steer a dynamical system from a certain initial state $\mathbf{x}_0$ to a desired target state $\mathbf{x}^*$ in finite time $T$. Recent advances in deep learning and neural network-based optimization have contributed to the development of methods that can help solve control problems involving high-dimensional dynamical systems. In particular, the framework of neural ordinary differential equations (neural ODEs) provides an efficient means to iteratively approximate continuous time control functions associated with analytically intractable and computationally demanding control tasks. Although neural ODE controllers have shown great potential in solving complex control problems, the understanding of the effects of hyperparameters such as network structure and optimizers on learning performance is still very limited. Our work aims at addressing some of these knowledge gaps to conduct efficient hyperparameter optimization. To this end, we first analyze how truncated and non-truncated backpropagation through time affect runtime performance and the ability of neural networks to learn optimal control functions. Using analytical and numerical methods, we then study the role of parameter initializations, optimizers, and neural-network architecture. Finally, we connect our results to the ability of neural ODE controllers to implicitly regularize control energy.

Spectrally Adapted Physics-Informed Neural Networks for Solving Unbounded Domain Problems

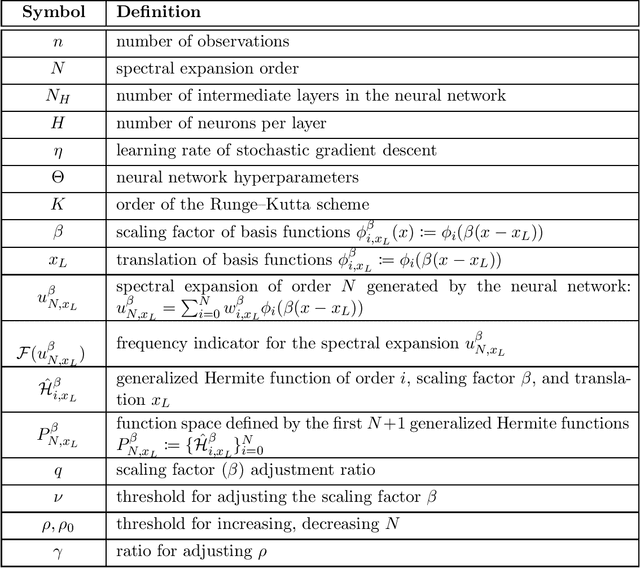
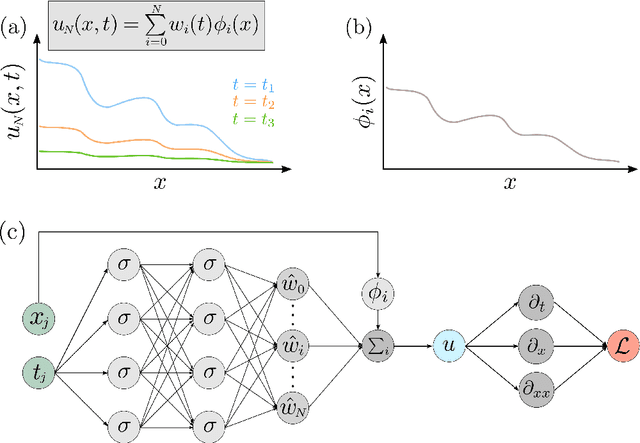
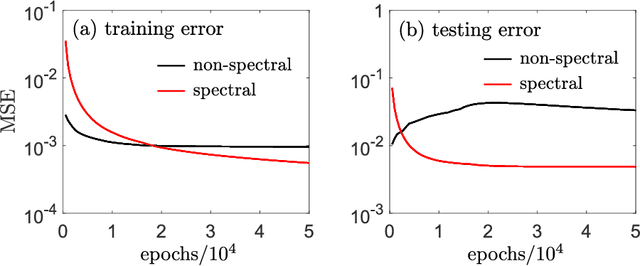
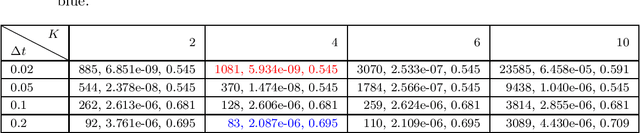
Solving analytically intractable partial differential equations (PDEs) that involve at least one variable defined in an unbounded domain requires efficient numerical methods that accurately resolve the dependence of the PDE on that variable over several orders of magnitude. Unbounded domain problems arise in various application areas and solving such problems is important for understanding multi-scale biological dynamics, resolving physical processes at long time scales and distances, and performing parameter inference in engineering problems. In this work, we combine two classes of numerical methods: (i) physics-informed neural networks (PINNs) and (ii) adaptive spectral methods. The numerical methods that we develop take advantage of the ability of physics-informed neural networks to easily implement high-order numerical schemes to efficiently solve PDEs. We then show how recently introduced adaptive techniques for spectral methods can be integrated into PINN-based PDE solvers to obtain numerical solutions of unbounded domain problems that cannot be efficiently approximated by standard PINNs. Through a number of examples, we demonstrate the advantages of the proposed spectrally adapted PINNs (s-PINNs) over standard PINNs in approximating functions, solving PDEs, and estimating model parameters from noisy observations in unbounded domains.

Solving Inventory Management Problems with Inventory-dynamics-informed Neural Networks

A key challenge in inventory management is to identify policies that optimally replenish inventory from multiple suppliers. To solve such optimization problems, inventory managers need to decide what quantities to order from each supplier, given the on-hand inventory and outstanding orders, so that the expected backlogging, holding, and sourcing costs are jointly minimized. Inventory management problems have been studied extensively for over 60 years, and yet even basic dual sourcing problems, in which orders from an expensive supplier arrive faster than orders from a regular supplier, remain intractable in their general form. In this work, we approach dual sourcing from a neural-network-based optimization lens. By incorporating inventory dynamics into the design of neural networks, we are able to learn near-optimal policies of commonly used instances within a few minutes of CPU time on a regular personal computer. To demonstrate the versatility of inventory-dynamics-informed neural networks, we show that they are able to control inventory dynamics with empirical demand distributions that are challenging to tackle effectively using alternative, state-of-the-art approaches.

Implicit energy regularization of neural ordinary-differential-equation control

Although optimal control problems of dynamical systems can be formulated within the framework of variational calculus, their solution for complex systems is often analytically and computationally intractable. In this Letter we present a versatile neural ordinary-differential-equation control (NODEC) framework with implicit energy regularization and use it to obtain neural-network-generated control signals that can steer dynamical systems towards a desired target state within a predefined amount of time. We demonstrate the ability of NODEC to learn control signals that closely resemble those found by corresponding optimal control frameworks in terms of control energy and deviation from the desired target state. Our results suggest that NODEC is capable to solve a wide range of control and optimization problems, including those that are analytically intractable.

NNC: Neural-Network Control of Dynamical Systems on Graphs

We study the ability of neural networks to steer or control trajectories of dynamical systems on graphs. In particular, we introduce a neural-network control (NNC) framework, which represents dynamical systems by neural ordinary different equations (neural ODEs), and find that NNC can learn control signals that drive networked dynamical systems into desired target states. To identify the influence of different target states on the NNC performance, we study two types of control: (i) microscopic control and (ii) macroscopic control. Microscopic control minimizes the L2 norm between the current and target state and macroscopic control minimizes the corresponding Wasserstein distance. We find that the proposed NNC framework produces low-energy control signals that are highly correlated with those of optimal control. Our results are robust for a wide range of graph structures and (non-)linear dynamical systems.

Learning the Ising Model with Generative Neural Networks

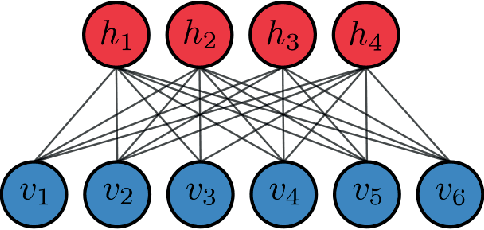
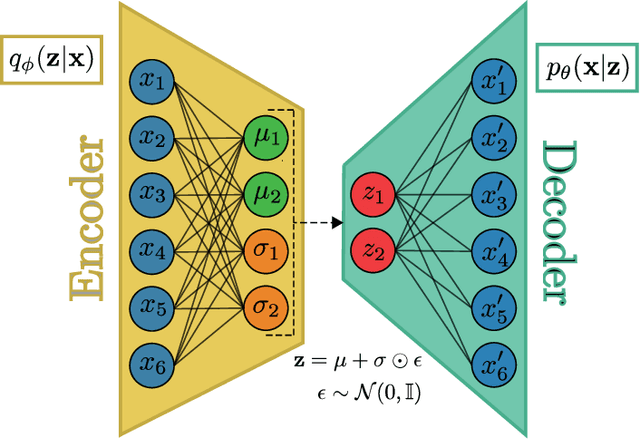
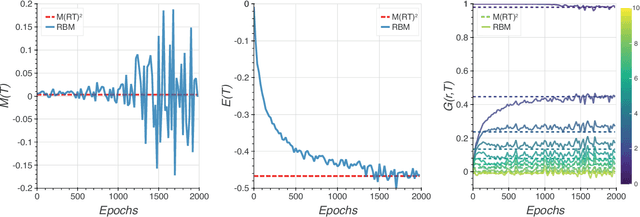
Recent advances in deep learning and neural networks have led to an increased interest in the application of generative models in statistical and condensed matter physics. In particular, restricted Boltzmann machines (RBMs) and variational autoencoders (VAEs) as specific classes of neural networks have been successfully applied in the context of physical feature extraction and representation learning. Despite these successes, however, there is only limited understanding of their representational properties and limitations. To better understand the representational characteristics of both generative neural networks, we study the ability of single RBMs and VAEs to capture physical features of the Ising model at different temperatures. This approach allows us to quantitatively assess learned representations by comparing sample features with corresponding theoretical predictions. Our results suggest that the considered RBMs and convolutional VAEs are able to capture the temperature dependence of magnetization, energy, and spin-spin correlations. The samples generated by RBMs are more evenly distributed across temperature than those of VAEs. We also find that convolutional layers in VAEs are important to model spin correlations.