Hierarchical RBF-KAN and RBF-SKAN Architectures for Multidimensional Function Approximation and Random Field Learning

In this manuscript, we propose and analyze hierarchical Kolmogorov--Arnold neural network architectures employing radial basis functions as activation functions for approximating deterministic functions and random field models. Specifically, we develop a hierarchical radial-basis-function Kolmogorov--Arnold network (hierarchical RBF-KAN) for multidimensional deterministic function approximation and a hierarchical radial-basis-function stochastic Kolmogorov--Arnold network (hierarchical RBF-SKAN) for random field learning. From a theoretical perspective, we establish universal approximation results for both architectures. In particular, we derive quantitative approximation estimates for the hierarchical RBF-KAN, showing that the proposed framework has the potential to partially alleviate the curse of dimensionality in learning high-dimensional functions by reducing the effective dimensionality of the approximation problem. Furthermore, we show that the hierarchical RBF-SKAN can approximate random field models under the Wasserstein-2 metric. Empirically, we show that our proposed radial-basis-function-based neural network structure could effectively learn multivariate functions and random field models.

Efficient reconstruction of multidimensional random field models with heterogeneous data using stochastic neural networks

In this paper, we analyze the scalability of a recent Wasserstein-distance approach for training stochastic neural networks (SNNs) to reconstruct multidimensional random field models. We prove a generalization error bound for reconstructing multidimensional random field models on training stochastic neural networks with a limited number of training data. Our results indicate that when noise is heterogeneous across dimensions, the convergence rate of the generalization error may not depend explicitly on the model's dimensionality, partially alleviating the "curse of dimensionality" for learning multidimensional random field models from a finite number of data points. Additionally, we improve the previous Wasserstein-distance SNN training approach and showcase the robustness of the SNN. Through numerical experiments on different multidimensional uncertainty quantification tasks, we show that our Wasserstein-distance approach can successfully train stochastic neural networks to learn multidimensional uncertainty models.

A new local time-decoupled squared Wasserstein-2 method for training stochastic neural networks to reconstruct uncertain parameters in dynamical systems

In this work, we propose and analyze a new local time-decoupled squared Wasserstein-2 method for reconstructing the distribution of unknown parameters in dynamical systems. Specifically, we show that a stochastic neural network model, which can be effectively trained by minimizing our proposed local time-decoupled squared Wasserstein-2 loss function, is an effective model for approximating the distribution of uncertain model parameters in dynamical systems. Through several numerical examples, we showcase the effectiveness of our proposed method in reconstructing the distribution of parameters in different dynamical systems.

A local squared Wasserstein-2 method for efficient reconstruction of models with uncertainty

In this paper, we propose a local squared Wasserstein-2 (W_2) method to solve the inverse problem of reconstructing models with uncertain latent variables or parameters. A key advantage of our approach is that it does not require prior information on the distribution of the latent variables or parameters in the underlying models. Instead, our method can efficiently reconstruct the distributions of the output associated with different inputs based on empirical distributions of observation data. We demonstrate the effectiveness of our proposed method across several uncertainty quantification (UQ) tasks, including linear regression with coefficient uncertainty, training neural networks with weight uncertainty, and reconstructing ordinary differential equations (ODEs) with a latent random variable.

An efficient Wasserstein-distance approach for reconstructing jump-diffusion processes using parameterized neural networks

We analyze the Wasserstein distance ($W$-distance) between two probability distributions associated with two multidimensional jump-diffusion processes. Specifically, we analyze a temporally decoupled squared $W_2$-distance, which provides both upper and lower bounds associated with the discrepancies in the drift, diffusion, and jump amplitude functions between the two jump-diffusion processes. Then, we propose a temporally decoupled squared $W_2$-distance method for efficiently reconstructing unknown jump-diffusion processes from data using parameterized neural networks. We further show its performance can be enhanced by utilizing prior information on the drift function of the jump-diffusion process. The effectiveness of our proposed reconstruction method is demonstrated across several examples and applications.

Squared Wasserstein-2 Distance for Efficient Reconstruction of Stochastic Differential Equations

We provide an analysis of the squared Wasserstein-2 ($W_2$) distance between two probability distributions associated with two stochastic differential equations (SDEs). Based on this analysis, we propose the use of a squared $W_2$ distance-based loss functions in the \textit{reconstruction} of SDEs from noisy data. To demonstrate the practicality of our Wasserstein distance-based loss functions, we performed numerical experiments that demonstrate the efficiency of our method in reconstructing SDEs that arise across a number of applications.

A Spectral Approach for Learning Spatiotemporal Neural Differential Equations

Rapidly developing machine learning methods has stimulated research interest in computationally reconstructing differential equations (DEs) from observational data which may provide additional insight into underlying causative mechanisms. In this paper, we propose a novel neural-ODE based method that uses spectral expansions in space to learn spatiotemporal DEs. The major advantage of our spectral neural DE learning approach is that it does not rely on spatial discretization, thus allowing the target spatiotemporal equations to contain long range, nonlocal spatial interactions that act on unbounded spatial domains. Our spectral approach is shown to be as accurate as some of the latest machine learning approaches for learning PDEs operating on bounded domains. By developing a spectral framework for learning both PDEs and integro-differential equations, we extend machine learning methods to apply to unbounded DEs and a larger class of problems.

Spectrally Adapted Physics-Informed Neural Networks for Solving Unbounded Domain Problems

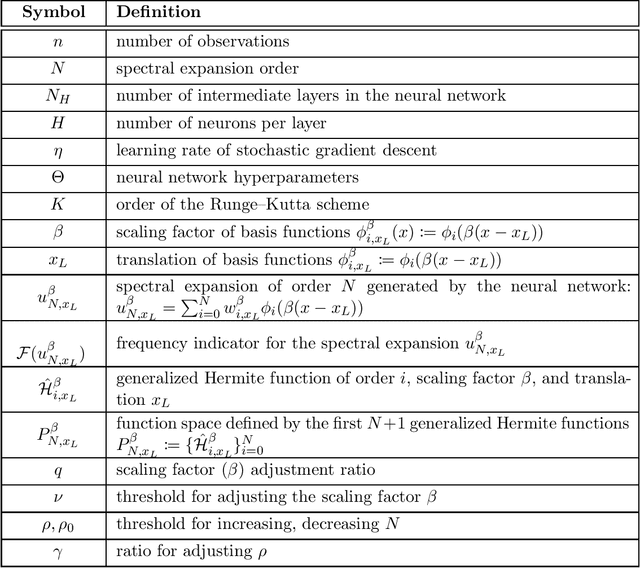
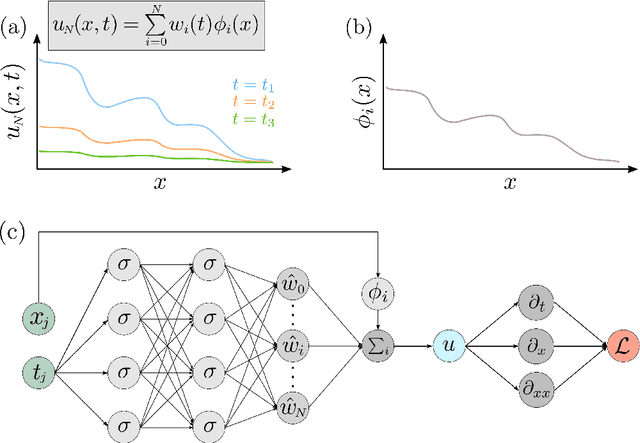
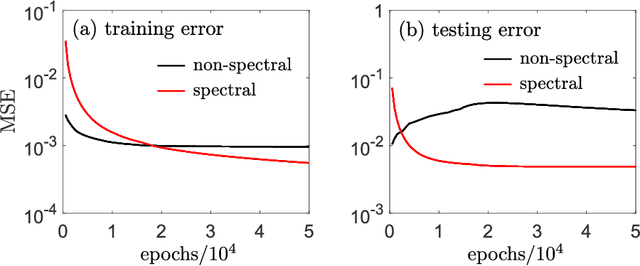
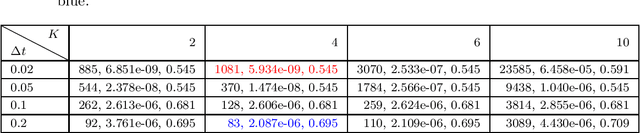
Solving analytically intractable partial differential equations (PDEs) that involve at least one variable defined in an unbounded domain requires efficient numerical methods that accurately resolve the dependence of the PDE on that variable over several orders of magnitude. Unbounded domain problems arise in various application areas and solving such problems is important for understanding multi-scale biological dynamics, resolving physical processes at long time scales and distances, and performing parameter inference in engineering problems. In this work, we combine two classes of numerical methods: (i) physics-informed neural networks (PINNs) and (ii) adaptive spectral methods. The numerical methods that we develop take advantage of the ability of physics-informed neural networks to easily implement high-order numerical schemes to efficiently solve PDEs. We then show how recently introduced adaptive techniques for spectral methods can be integrated into PINN-based PDE solvers to obtain numerical solutions of unbounded domain problems that cannot be efficiently approximated by standard PINNs. Through a number of examples, we demonstrate the advantages of the proposed spectrally adapted PINNs (s-PINNs) over standard PINNs in approximating functions, solving PDEs, and estimating model parameters from noisy observations in unbounded domains.