An efficient Wasserstein-distance approach for reconstructing jump-diffusion processes using parameterized neural networks

We analyze the Wasserstein distance ($W$-distance) between two probability distributions associated with two multidimensional jump-diffusion processes. Specifically, we analyze a temporally decoupled squared $W_2$-distance, which provides both upper and lower bounds associated with the discrepancies in the drift, diffusion, and jump amplitude functions between the two jump-diffusion processes. Then, we propose a temporally decoupled squared $W_2$-distance method for efficiently reconstructing unknown jump-diffusion processes from data using parameterized neural networks. We further show its performance can be enhanced by utilizing prior information on the drift function of the jump-diffusion process. The effectiveness of our proposed reconstruction method is demonstrated across several examples and applications.

Gradient-flow adaptive importance sampling for Bayesian leave one out cross-validation for sigmoidal classification models

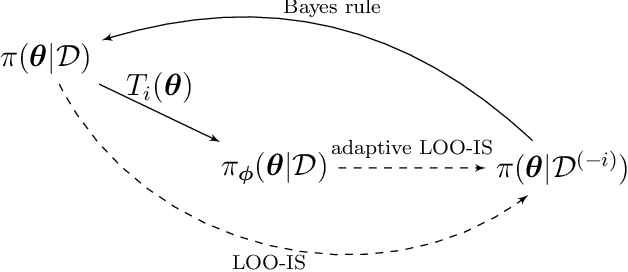
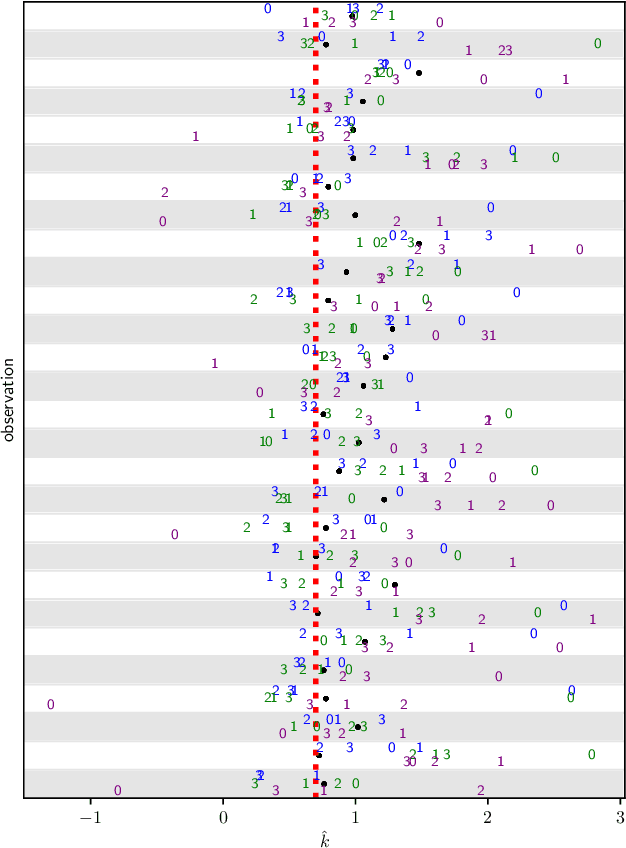
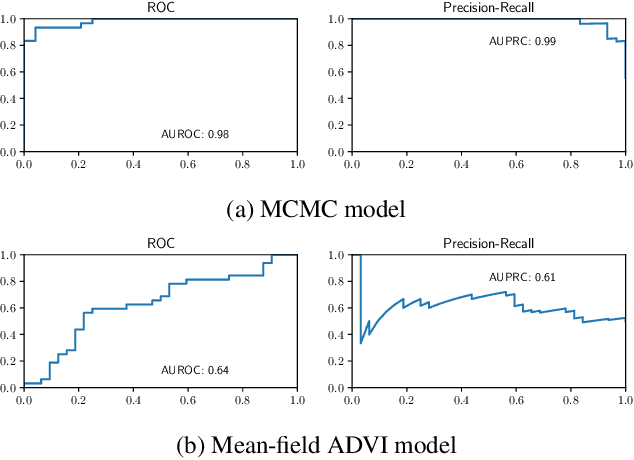
We introduce a set of gradient-flow-guided adaptive importance sampling (IS) transformations to stabilize Monte-Carlo approximations of point-wise leave one out cross-validated (LOO) predictions for Bayesian classification models. One can leverage this methodology for assessing model generalizability by for instance computing a LOO analogue to the AIC or computing LOO ROC/PRC curves and derived metrics like the AUROC and AUPRC. By the calculus of variations and gradient flow, we derive two simple nonlinear single-step transformations that utilize gradient information to shift a model's pre-trained full-data posterior closer to the target LOO posterior predictive distributions. In doing so, the transformations stabilize importance weights. Because the transformations involve the gradient of the likelihood function, the resulting Monte Carlo integral depends on Jacobian determinants with respect to the model Hessian. We derive closed-form exact formulae for these Jacobian determinants in the cases of logistic regression and shallow ReLU-activated artificial neural networks, and provide a simple approximation that sidesteps the need to compute full Hessian matrices and their spectra. We test the methodology on an $n\ll p$ dataset that is known to produce unstable LOO IS weights.

Squared Wasserstein-2 Distance for Efficient Reconstruction of Stochastic Differential Equations

We provide an analysis of the squared Wasserstein-2 ($W_2$) distance between two probability distributions associated with two stochastic differential equations (SDEs). Based on this analysis, we propose the use of a squared $W_2$ distance-based loss functions in the \textit{reconstruction} of SDEs from noisy data. To demonstrate the practicality of our Wasserstein distance-based loss functions, we performed numerical experiments that demonstrate the efficiency of our method in reconstructing SDEs that arise across a number of applications.

A Spectral Approach for Learning Spatiotemporal Neural Differential Equations

Rapidly developing machine learning methods has stimulated research interest in computationally reconstructing differential equations (DEs) from observational data which may provide additional insight into underlying causative mechanisms. In this paper, we propose a novel neural-ODE based method that uses spectral expansions in space to learn spatiotemporal DEs. The major advantage of our spectral neural DE learning approach is that it does not rely on spatial discretization, thus allowing the target spatiotemporal equations to contain long range, nonlocal spatial interactions that act on unbounded spatial domains. Our spectral approach is shown to be as accurate as some of the latest machine learning approaches for learning PDEs operating on bounded domains. By developing a spectral framework for learning both PDEs and integro-differential equations, we extend machine learning methods to apply to unbounded DEs and a larger class of problems.